CORRELATED SYSTEMS

Anderson localization versus nonlinear interactions

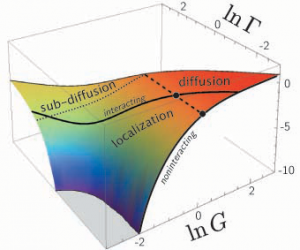In a strong enough disorder, quantum particles interfere destructively and undergo Anderson localization, which features a complete halt of wave diffusion. In dimension 3, localization occurs when the particle’s energy becomes smaller than a critical value, the mobility edge, to which is associated a phase transition called the Anderson transition. Experimentally, the latter can be observed by letting a matter wave packet expand in an optical speckle: below the critical energy, the wave-packet spreading is frozen at long times.

What happens if now the particles interact with one another? For a weakly interacting matter wave packet described by the Gross-Pitaevskii equation, we have shown that interactions drastically change the nature of the Anderson transition. Indeed, while diffusion as well as the mobility edge remain unaffected by interactions to leading order, the latter destroy localization and replace it by a regime of subdiffusive transport. In other words, the Anderson transition becomes a sub-diffusion/diffusion transition, characterized by original properties and especially by a novel critical exponent [1]. Intuitively, the alteration of the Anderson transition appears because each particle feels the (nonlinear) potential created by all others. This potential modifies their phase, and eventually their ability to interfere and thus to localize.

More recently, we have also studied the complementary problem of matter-wave propagation in momentum space. In this setup, weak interactions treated within a mean-field approach lead to a thermalization of the matter-wave momentum distribution [2].

Strongly correlated systems

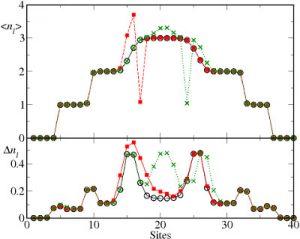This research activity concerns the theoretical study of many-body systems formed by ultracold atom gases in optical lattices. Ultracold atoms in optical lattices, initially considered an “experimental toy model” for condensed matter physics, have recently become an independent field of research, central in the physics of complex quantum systems. They are efficiently described by a Bose-Hubbard model, which shows similarity to the Hubbard model first used to model a gas of electrons in a solid body. Atoms forming the ultracold gas interact through collisions which may not be neglected: the Mott insulator phase, present in low-mobility regime, is a direct consequence of the presence of interactions. Ability to change the system parameters by adjusting the strength of lasers enables to realize different regimes and to explore the phase transitions and the crossovers between them. In this context, the description of the many-body problem must be done exactly, in a true many-body way.
Such systems pose a serious challenge from the computational point of view, due to their large degree of entanglement. However, the restriction of the problem geometry to 1D enables to preserve the many-bodyness and the complex nature of these systems, providing at the same time a very powerful computational tool : the DMRG approach and related techniques. This is due to the area laws satisfied by 1D systems, which limit the entanglement and enable an efficient analysis of systems consisting of hundreds of particles. Among other works, we have recently used the DMRG approach to numerically compute the many-body eigenvectors of a strongly correlated system [1], and have analyzed the effects of the inclusion of higher Bloch bands on the dynamics [2].