Squeezing multimode quantum states to enhance sensor networks
The probabilistic nature of quantum mechanics usually prevents us from predicting with certainty the result of a single measurement. These so-called quantum fluctuations lead to measurement noise that limits the precision of any measurement, even after all sources of technical noise have been eliminated, e.g., by isolating the experimental setup from its environment.
To overcome the precision limit imposed by measurement noise, the field of quantum metrology explores the potential offered by ideas from quantum information theory. For example, by engineering non-classical quantum states, it is possible to reduce the quantum fluctuations in the measurement observable at the expense of those in another observable that is of no interest to the measurement. This technique, known as squeezing, is used today to improve the sensitivity of gravitational wave detectors and atomic clocks and interferometers. In these experiments, a single phase parameter is measured with the highest possible precision.
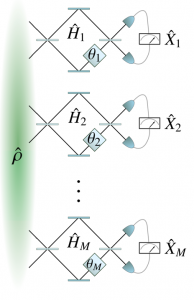
Figure 1. Schematic representation of a sensor network based on M parallel interferometers. Each interferometer captures a different parameter. The sensitivity of a collective estimation of all parameters can be enhanced by the squeezing of the local measurement observables and by quantum correlations between the interferometers.
Having established a rather good understanding of the theory of quantum metrology of single parameters, researchers have recently started to address the question of the ultimate precision limits for sensor networks that measure multiple parameters simultaneously. This problem is of high relevance for the development of quantum-enhanced imaging methods and the measurement of spatially distributed electromagnetic fields and gradients. However, fundamental limitations of the existing theoretical framework make it very hard to identify the precision limits in general scenarios.
In our recent collaboration between LKB and researchers from the CNR (Florence, Italy) we have developed a theoretical method that characterizes the squeezing of multiple quantum observables. The sensitivity gain that can be obtained in a multiparameter measurement is expressed in terms of a squeezing matrix that captures the errors of all parameters and the correlations between them. Our work establishes necessary theoretical tools to understand the potential of squeezed states in multimode systems for quantum-enhanced multiparameter measurements. It further provides a practical approach for the development of sensor networks based on atomic and optical quantum systems.
