Femtosecond Quantum Information
TEAM MEMBERS
PERMANENT STAFF
- Claude Fabre
- Nicolas Treps
- Valentina Parigi
- Mattia Walschaers
POSTDOC
- Alex Davis
- Srinivasan Kaali
- Giacomo Sorelli
PHD STUDENT
- Matthieu Ansquer
- Paul Renault
- Tiphaine Kouadou
- Ganaël Roeland
- Francesca Sansavini
Quantum Frequency Combs
Ultrafast pulses are beginning to exhibit an increasingly important role in quantum optics and quantum information science due to their inherently unique temporal and spectral structure. For instance, entanglement amongst multiple modes is necessary for implementation of current quantum information protocols in the continuous-variable regime (e.g., as in one-way quantum computing with cluster states). The traditional means for generation of such multimode states is to sequentially mix together individual continuous-wave laser beams exhibiting the desired quantum properties. While successful for a small number of modes, this scheme is clearly not scable as it necessitates an ever-increasing number of optical elements (i.e., an individual cavity for each mode, beam-splittes to mix the modes, etc.). An alternative approach is to begin with a light source that is intrinsically multimode. Toward this end, femtosecond pulses of light contain upwards of 10^5 individual frequencies in a single beam. The introduction of these pulses into a device capable of coupling several frequency modes through a nonlinear interaction produces an entangled, multimode output. Indeed, recent work has demonstrated the use of a synchronously pumped optical parametric oscillator (SPOPO) to generate multimode nonclassical states of light [Roselund2014]
The Femto Lab Team works on 2 main projects :
Quantum Information Protocols
Publications
- Y. Cai, J. Roslund, G. Ferrini, F. Arzani, X. Xu, C. Fabre & N. Treps, Multimode entanglement in reconfigurable graph states using optical frequency combs, Nature Communications 8, 15645 (2017)
- Roslund, J., De Araujo, R. M., Jiang, S., Fabre, C., & Treps, N. (2014). Wavelength-multiplexed quantum networks with ultrafast frequency combs. Nature Photonics, 8(2), 109-112.
- R. Medeiros de Araújo, J. Roslund, Y. Cai, G. Ferrini, C. Fabre, and N. Treps. Full characterization of a highly multimode entangled state embedded in an optical frequency comb using pulse shaping. Phys. Rev. A 89, 053828 (arXiv:1401.4867)
- S. Gerke, J. Sperling, W. Vogel, Y. Cai, J. Roslund, N. Treps, and C. Fabre. Full multipartite entanglement of frequency comb Gaussian states. Phys. Rev. Lett. 114, 050501 ( arXiv:1409.5692)
- Giulia Ferrini, Jean-Pierre Gazeau, Thomas Coudreau, Claude Fabre, Nicolas Treps. Compact Gaussian quantum computation by multi-pixel homodyne detection 2013 New J. Phys. 15
- G. Ferrini, J. Roslund, F. Arzani, Y. Cai, C. Fabre, and N. Treps. Optimization of networks for measurement-based quantum computation
- Valentin A. Averchenko, Valérian Thiel, and Nicolas Treps. Non-linear photon subtraction from a multimode quantum field. Phys. Rev. A 89, 063808 (arXiv:1404.0160)
- Arzani F, Fabre C and Treps N 2018 Versatile engineering of multimode squeezed states by optimizing the pump spectral profile in spontaneous parametric down-conversion Phys. Rev. A 97033808
- Young-Sik Ra, Clément Jacquard, Adrien Dufour, Claude Fabre, and Nicolas Treps Phys. Rev. X 7, 031012 – Published 19 July 2017
The output of a syncronously pumped optical parametric oscillator (SPOPO) embeds a multimode non-classical state of light in which different frequencies share quantum correlations, i.e. they are entangled. This is due to the fact that the SPOPO act as an ensemble of independent squeezers on a set of modes with a broad spectral profile. Shifting to a description of the state in terms of frequency bands is then equivalent to a linear optical transformation introducing quantum correlations. Entanglement being a central resource in quantum information theory, this renders the SPOPO a good candidate system for the implementation of quantum information processing tasks. The main advantage comes from the fact that, while it is often difficult to create entanglement over a large number of components, in the case of the SPOPO the entire multimode state is produced in one single step and is contained in one beam, making the resource very compact and scalable. Indeed, experiments conducted by our group already demonstrated the full quantum entanglement of up to ten spectral bands , and hundreds of modes are potentially addressable [1, 2, 3].We tackle the problem of using the SPOPO for information processing both exeprimentally and theoretically.
MQBC
As the first example, the opportunity of turning the SPOPO into a measurement based quantum computation (MBQC) [4] device in the continuous-variable (CV) regime [5] has been studied [6].
Measurement based quantum computation (or One Way Quantum Computing) is a paradigm for quantum computing where all the effort is put into the production of a highly correlated multimode state (cluster state), and processing is then done by simple projective measurement on the nodes of that state.
Most often, the creation of multimode entangled state such as cluster states in a quantum optical setup requires a network of beam-splitters and dephasers, which transform the squeezed input modes in entangled output modes [7]. The configuration of this network varies considerably with the state to be generated, and its complexity grows rapidly with the number of modes, which renders this method poorly scalable.
The SPOPO, however, has the advantage of producing this multimode entangled state in one step.
![]()
The produced state is also tunable via pump shaping [15]. The suitable modes should then be measured to process information. To this end, we developed a multi-pixel homodyne detection system. The computation is then completed with a digital post-processing stage of the acquired signals. This allows to obtain a simultaneous measure of e.g. the amplitude quadrature on all the modes in a chosen mode basis.
Read more
It is to be noticed that the transformation which brings from the input modes to the modes can be modeled as a unitary matrix (UT), acting on the vector which regroups the annihilation operators associated to the various squeezed input modes (aSQU). The digital recombination leads to a second transformation, which can be described by an orthogonal matrix O. Finally, two other operations on the modes are possible, which can be modeled independently. First, a possible shaping of the local oscillator would correspond to a matrix DLO multiplying the homodyne detection matrix UT. On the other side, a relative dephasing between the input modes, corresponding to the choice of the quadrature of each mode which is squeezed, is modeled by a diagonal matrix DR acting on the modes aSQU. This is summarized by the following figure
In summary, this method allows for the realization of unitaries on the (possibly numerous) modes in a more compact and efficient way compared to the beam-splitter network, and can be therefore exploited for the simultaneous creation and measurement of cluster states, yielding a gaussian quantum computation.
MBQC in the CV regime was first formulated in terms of ideal infinitely-squeezed states. Being equivalent to perfectly monochromatic waves in mechanical systems, these carry infinite energy and can only be approximated in realistic implementations with highly but finitely squeezed states. It can be shown that this amounts to introducing computation errors. Our group recently proposed a method to mitigate these errors when asymmetric squeezing is present in the modes used to generate the entangled resource [8]. This method directly applies to the SPOPO setup but may also be used in any other physical scheme for the production of cluster states.
For universal (and any faster than classical) quantum computation, the use of more than quadratic (non-gaussian) nonlinearities is required. It is essential then to introduce non gaussian elements in the experiment. Single-photon operations, as photon counting detectors or single photon addition or subtraction, are among the simplest to achieve practically.
To this end, we demonstrated mode-dependent photon subtraction through sum frequency generation theoretically and experimentally [9, 16].
Motivated by this, we are also interested in the characterization of the protocols that may be implemented with such resources. These include sub-universal computations (as e.g. boson sampling) and polynomial approximation of unitary non-gaussian gates.
Boson sampling [10] is a protocol exploiting the bosonic statistics of photons to compute the permanent of a unitary matrix, that can represent a linear optical network, a problem which is believed to be classically hard. The interest in this kind of problems is due to the fact that they represent a demonstration of the “better-than-classical” performances allowed exploiting quantum mechanics and the optical setups required are usually much simpler than those necessary for fully universal quantum computation.
Polynomial approximation of unitary gates recently gained some attention due to the practical difficulties of introducing non-gaussian evolution to the state of a light beam by traditional approaches such as high-order optical nonlinearities and photon-counting. In contrast to that, protocols have been proposed for the polynomial approximation of gates using only on/off photodetection on gaussian states or single photon sources and gaussian measurements [11, 12, 13].
Secret sharing:
Other possible applications of the SPOPO for quantum information processing include secret-sharing protocols. Secret-sharing consists in sending an encoded message to a group of n players in such a way that at least k players need to collaborate in order to faithfully reconstruct the original message (this schemes are more precisely called (n,k) threshold schemes). Classical protocols exist to do this, but quantum correlations can also be exploited to enhance the quality of the retrieved message [14].
Gaussian verification of continuous-variable quantum states
Our experimental set-up is composed of 3 main parts:
– The SPOPO which produces a multimode gaussian state and is tunable via pump spectral shaping.
– The coherent mode-selective single photon subtractor which implements a non-gaussian operation and is tunable via gate spectral shaping.
– The homodyne detection which is used to measure quadratures of the state in a particular mode and is tunable via Local Oscillator spectral shaping.
These three parts may be considered as separate parties (Alice, Bob, Charlie) involved in a communication or computation protocol.
For example, Alice may control the SPOPO and homodyne detection and Bob the subtractor. Alice may ask Bob to perform a non-gaussian operation on a gaussian state she produces. Then one may ask how Alice can verify whether the operation she requested was indeed performed by Bob.
The set-up can therefore be used as a tool to implement proof of principle for protocols of Cloud/Distributed Quantum computing.
In this context, we are working in collaboration with LIP6 to develop and implement such protocols.
First protocol:
In this protocol, a first party (Alice) asks another party (Bob) to produce and send a non-gaussian CV state . Bob is not trusted, and Alice needs to verify the soundness of the state. Alice can measure the state produced with a heterodyne detection and she needs to find a good estimator of the fidelity , where is the (pure) quantum state required by Alice and is the state effectively sent by Bob.
The protocol works as follows:
– Bobs send M states.
– Using a De Finetti reduction and discarding a fraction of these M states, we can extract a subset of N output states that can be considered as independent and identically distributed.
– Alice measures all the states but one, chosen at random, with heterodyne detection.
– Alice perform an energy test to restrict the dimension of the output phase space.
– Using quasi-probability distribution formalism, we approximate the fidelity with an estimator that can be computed for i.i.d. Bob with high probability using her sample.
Using the Hoeffding bound, the distance can be upper bounded, therefore providing a security criterion.
– If the fidelity estimate is close to 1 Alice accepts the state, she rejects otherwise.
References
- [1] Roslund, J., De Araujo, R. M., Jiang, S., Fabre, C., & Treps, N. (2014). Wavelength-multiplexed quantum networks with ultrafast frequency combs. Nature Photonics, 8(2), 109-112
- [2] R. Medeiros de Araújo, J. Roslund, Y. Cai, G. Ferrini, C. Fabre, and N. Treps. Full characterization of a highly multimode entangled state embedded in an optical frequency comb using pulse shaping. Phys. Rev. A 89, 053828 (arXiv:1401.4867)
- [3] S. Gerke, J. Sperling, W. Vogel, Y. Cai, J. Roslund, N. Treps, and C. Fabre. Full multipartite entanglement of frequency comb Gaussian states. Phys. Rev. Lett. 114, 050501 ( arXiv:1409.5692)
- [4] J. Briegel and R. Raussendorf, Phys. Rev. Lett. 86, 910 (2001) ; R. Raussendorf and H.J. Briegel, Phys. Rev. Lett. 86, 5188 (2001)
- [5] M. Gu et al, Phys. Rev. A 79, 062318 (2009).
- [6] Giulia Ferrini, Jean-Pierre Gazeau, Thomas Coudreau, Claude Fabre, Nicolas Treps. Compact Gaussian quantum computation by multi-pixel homodyne detection 2013 New J. Phys. 15 093015 (arXiv:1303.5355)
- [7] R. Ukai et al, Phys. Rev. Lett. 106, 240504 (2011).
- [8] G. Ferrini, J. Roslund, F. Arzani, Y. Cai, C. Fabre, and N. Treps. Optimization of networks for measurement-based quantum computation. Phys. Rev. A.
- [9] Valentin A. Averchenko, Valérian Thiel, and Nicolas Treps. Non-linear photon subtraction from a multimode quantum field. Phys. Rev. A 89, 063808 (arXiv:1404.0160)
- [10] Aaronson, S., & Arkhipov, A. (2011, June). In Proceedings of the forty-third annual ACM symposium on Theory of computing (pp. 333-342). ACM.
- [11] Petr Marek, Radim Filip, and Akira Furusawa. Phys. Rev. A 84, 053802
- [12] Kimin Park, Petr Marek, and Radim Filip. Phys. Rev. A 90, 013804
- [13] Kevin Marshall, Raphael Pooser, George Siopsis, Christian Weedbrook, arXiv:1412.0336
- [14] Andrew M Lance et al 2003 New J. Phys. 5 4
- [15] Arzani F, Fabre C and Treps N 2018 Versatile engineering of multimode squeezed states by optimizing the pump spectral profile in spontaneous parametric down-conversion Phys. Rev. A 97033808
- [16] Y-S. Ra et. al. PRX 7, 031012 (2017)
- [17] Y-S. Ra et. al. Reconfigurable non-Gaussian multimode states of quantum light … Coming soon.
Multimode Non-Gaussian states
Publications
- V. A. Averchenko, V. Thiel, and N. Treps, “Nonlinear photon subtraction from a multimode quantum field”, Phys. Rev. A 89, 063808 (2014).
- Y.-S. Ra, C. Jacquard, A. Dufour, C. Fabre, and N. Treps “Tomography of a Mode-Tunable Coherent Single-Photon Subtractor” Phys. Rev. X7, 031012 (2017).
- M. Walschaers, C. Fabre, V. Parigi, and N. Treps, “Entanglement and Wigner Function Negativity of Multimode Non-Gaussian States”, Phys. Rev. Lett.119, 183601 (2017).
- M. Walschaers, S. Sarkar, V. Parigi, and N. Treps “Tailoring Non-Gaussian Continuous-Variable Graph States” Phys. Rev. Lett.121, 220501 (2018).
-
M. Walschaers,C. Fabre, V. Parigi, and N. Treps “Statistical signatures of multimode single-photon-added and -subtracted states of light” Phys. Rev. A 96, 053835 (2017).
Continuous-variable quantum optics is a fruitful playground for quantum information processes. Via quantum frequency combs, we have access to quantum light with a vast number of entangled degrees of freedom. To generate the quantum frequency combs, we inject femtosecond pulses into a device capable of coupling several frequency modes through a nonlinear interaction produces an entangled, multimode output. Recent work has demonstrated the use of a synchronously pumped optical parametric oscillator (SPOPO) to generate multimode nonclassical states of light [Pinel 2012] in which the entanglement properties can be tuned [Roslund 2014, Cai 2017].
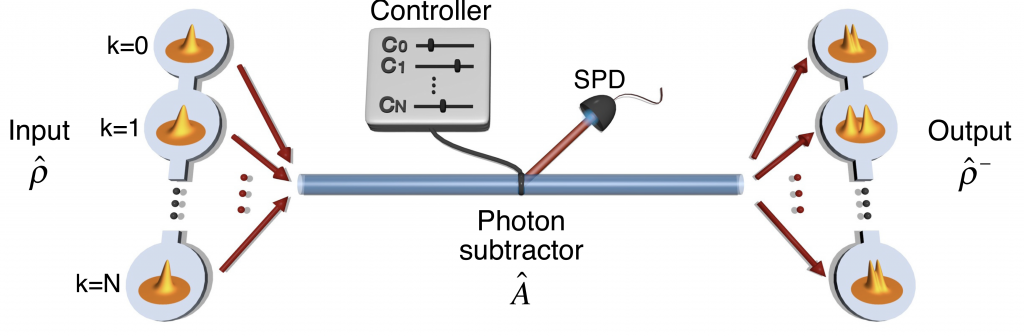
However, entangled nonclassical states of light are insufficient to reach a quantum computation advantages, since their quadrature measurements (i.e. the measurement of the complex amplitude of the electric field) are efficiently simulated on a standard classical computer. The missing ingredient to reach such a quantum advantage is a non-Gaussian operation that can distort the Gaussian measurement statistics of quadratures and even induce negative Wigner functions. We experimentally implement this non-Gaussian operation via mode-selective photon-subtraction [Averchenko 2014, Ra 2017]. This allows us to shape and characterize multimode non-Gaussian quantum states for quantum information purposes [Walschaers 2017, 2018].
References
- [Pinel 2012] O. Pinel, P. Jian, R. Medeiros de Araújo, J. Feng, B. Chalopin, C. Fabre, and N. Treps “Generation and Characterization of Multimode Quantum Frequency Combs”, Phys. Rev. Lett. 108, 083601 (2012).
- [Roslund 2014] J. Roslund, R. Medeiros de Araújo, S. Jiang, C. Fabre, and N. Treps, “Wavelength-multiplexed quantum networks with ultrafast frequency combs”, Nat. Photonics8, 109-112 (2014).
- [Cai 2017] Y. Cai, J. Roslund, G. Ferrini, F. Arzani, X. Xu, C. Fabre, and N. Treps, “Multimode entanglement in reconfigurable graph states using optical frequency combs”, Nat. Commun.8, 15645 (2017)
- [Averchenko 2014] V. A. Averchenko, V. Thiel, and N. Treps, “Nonlinear photon subtraction from a multimode quantum field”, Phys. Rev. A89, 063808 (2014).
- [Ra 2017] Y.-S. Ra, C. Jacquard, A. Dufour, C. Fabre, and N. Treps “Tomography of a Mode-Tunable Coherent Single-Photon Subtractor” Phys. Rev. X7, 031012 (2017).
- [Walschaers 2017] M. Walschaers, C. Fabre, V. Parigi, and N. Treps, “Entanglement and Wigner Function Negativity of Multimode Non-Gaussian States”, Phys. Rev. Lett.119, 183601 (2017)
- [Walschaers 2018] M. Walschaers, S. Sarkar, V. Parigi, and N. Treps “Tailoring Non-Gaussian Continuous-Variable Graph States” Phys. Rev. Lett.121, 220501 (2018).
