We are no longer considering new applications!
Light offers a vast potential in the development of modern quantum technologies due to its intrinsic resilience to decoherence effects that tend to scramble quantum information in matter-based setups. One avenue for employing light to process quantum information focuses on the continuous variable regime, where the observables of interest are the quadratures of the electric field. These continuous variables have proven their worth as a platform for creating huge entangled states (entangling up to one million optical modes). Additionally, this entanglement can be created in a deterministic fashion, and the resulting states are easily manipulated with standard techniques in optics [1,2]
To reach a quantum advantage, and perform a task that cannot be efficiently simulated with a classical device, we require more than just entanglement. The additional ingredient is non-Gaussian statistics in the outcomes of the quadrature measurements. More specifically, we must create quantum states with a negative Wigner functions. At LKB, we have recently developed a mode-tunable photon subtractor as a device for creating such states [3,4]. As such, we now have the possibility to produce large entangled states and to render them non-Gaussian. This opens up a whole new realm of research, where a vast amount of questions on the interplay between entanglement and non-Gaussian effects remain unanswered [4,5]. Within this internship, we will explore some of these questions.
In particular, we will investigate the interplay between non-Gaussian aspects of quantum states and quantum steering (also known as Einstein-Podolsky-Rosen steering). The latter is a special feature of certain quantum correlations, and is in some sense “stronger” than quantum entanglement. In general, when two subsystems, A (Alice) and B (Bob) are correlated, a measurement on A improves the precision of predictions for a measurement on B. In classical statistical theories, there are limits on the amount of information that can be extracted in this way. However, in quantum physics, these limits can be overcome, and in some cases we can find quantum correlations that allow us to make predictions about system B that are more precise than possible with any classical correlation. Such quantum correlations are said to be steerable, and A is said to be able to steer B. In continuous variable quantum optics, a profound example of a steerable quantum correlation can be found in Einstein-Podolsky-Rosen states.
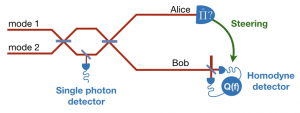
Steering through non-Gaussian entanglement
The internship offers two possible directions of research to probe how quantum steering and non-Guassian effects are intertwined:
- On the one hand, we explore how Gaussian quantum states with steerable quantum correlations react to non-Gaussian operations such as photon subtraction. This part will be an extension of previous work [5] done by the group.
- On the other hand, we explore how quantum states with manifestly non-Gaussian entanglement can be steered in a systematic way (see Figure). Brute force numerical methods are available to check whether a state is steerable or not, but our goal is rather to acquire an analytical understanding that allows us to learn something about the properties of these non-Gaussian states.
Finally, we will explore the possible connection between non-Gaussian entanglement and remote preparation of negativity of the Wigner function. The above figure shows the scenario where all the entanglement between Alice and Bob is non-Gaussian. However, we might consider modifying the beam splitter after the single-photon detector, such that Alice and Bob are working in a different basis. In this sense, it is an important question what are the signatures of non-Gaussian entanglement in different mode bases. This may potentially make it possible to experimentally observe non-Gaussian entanglement and steering.
Practical aspects: The starting and ending dates of the internship are flexible, but the project is intended to last between three and six months (depending on the candidates prior knowledge in quantum optics). Ideally the internship will either end before or start after august 2020, in accordance with the organisation of the academic year in France.
Subsequent PhD possibilities: The subject of non-Gaussian states in quantum optics is vast, and interested student who choose this project have the possibility to apply for a PhD position in the group. Even though the internship is mainly theoretical, a potential PhD can also involve experimental work in the multimode quantum optics group.
Contact: Mattia Walschaers
[1] J. Roslund, R. M. de Araujo, S. Jiang, C. Fabre, N. Treps, “Wavelength-multiplexed quantum networks with ultrafast frequency combs”, Nature Photonics 8, 109 (2014).
[2] Y. Cai, J. Roslund, G. Ferrini, F. Arzani, X. Xu, C. Fabre, N. Treps, “Multimode entanglement in reconfigurable graph states using optical frequency combs”, Nature Communication 8, 15645 (2017).
[3] Y.-S. Ra, C. Jacquard, A. Dufour, C. Fabre, N. Treps, “Tomography of a Mode-Tunable Coherent Single-Photon Subtractor” Phys. Rev. X, 7, 031012 (2017).
[4] Y.-S. Ra, A Dufour, M. Walschaers, C. Jacquard, T. Michel, C. Fabre, N. Treps, Non-Gaussian quantum states of a multimode light field, arXiv preprint arXiv:1901.10939, accepted Nat Physics
[5] M. Walschaers and N. Treps, Remote generation of Wigner-negativity through Einstein-Podolsky-Rosen steering, arXiv preprint arXiv:1912.02778.