Quantum Complex networks
Continuous Variables
Quantum Complex Networks
ERC grant COQCOoN
Valentina Parigi
At different scales,from molecular systems to technological infrastructures, physical systems group in structures which are neither simply regular or random, but can be represented by networks with complex shape. Proteins in metabolic structures and the World Wide Web, for example, share the same kind of statistical distribution of connections of their constituents. In addition, the individual elements of natural samples, like atoms or electrons, are quantum objects. Hence replicating complex networks in a scalable quantum platform is a formidable opportunity to learn more about the intrinsic quantumness of real world and for the efficient exploitation of quantum-complex structures in future technologies. Future trusted large-scale communications and efficient big data handling, in fact, will depend on at least one of the two aspects -quantum or complex- of scalable systems, or on an appropriate combination of the two.
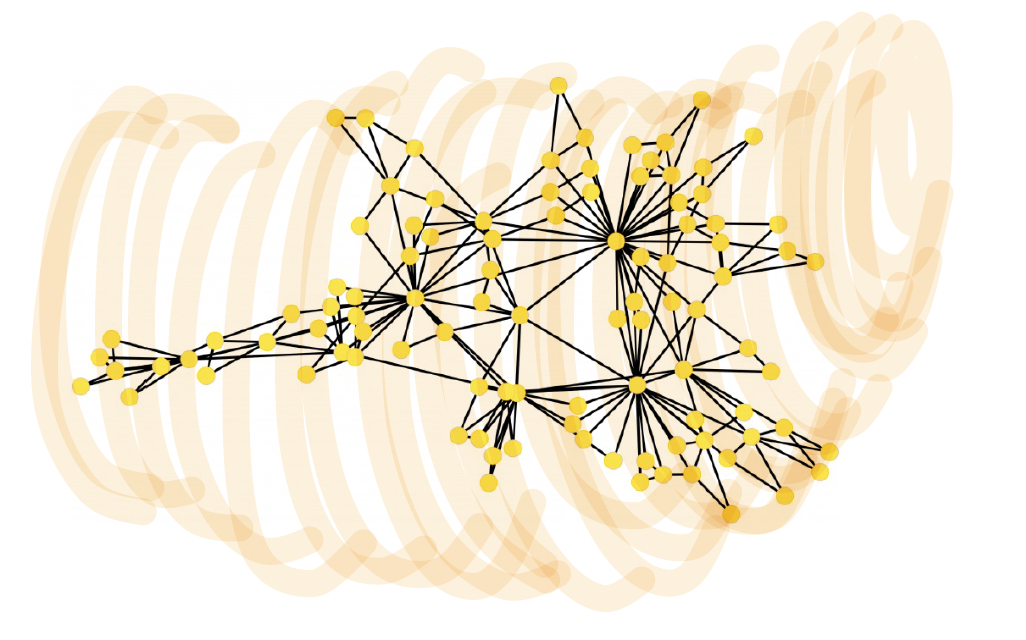
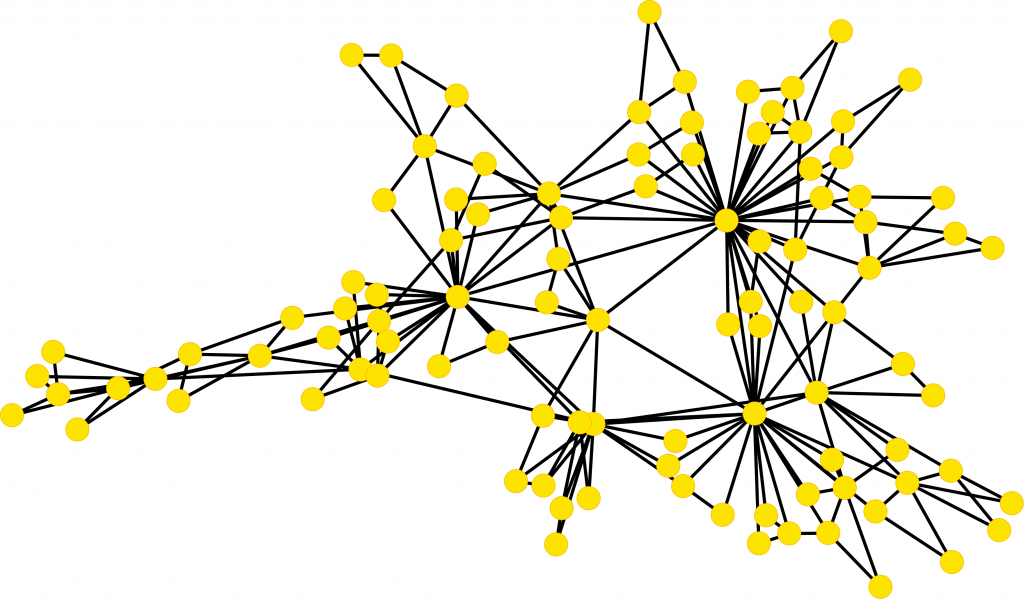 Growing networks constructed by addition of connected complexes of dimension 2, i.e. triangles ( Z. Wu et al. Scientific Reports 5, 10073 (2015)). The network is composed of 100 nodes, single links are added with hopping probability p=0.1, any link can belong to a large number (m) of triangles. The network shows community structures
Growing networks constructed by addition of connected complexes of dimension 2, i.e. triangles ( Z. Wu et al. Scientific Reports 5, 10073 (2015)). The network is composed of 100 nodes, single links are added with hopping probability p=0.1, any link can belong to a large number (m) of triangles. The network shows community structures
We investigate theory and experimental implementation of quantum complex networks in the framework of continuous variables encoding of quantum resources.
Multimode quantum resources based on parametric process, femtosecond laser along with mode-selective and multimode homodyne measurements, allows for the implementation of networks with reconfigurableall-to-all coupling and topology, with sufficient size and diversity to be relevant in the context of complex networks. We can deterministically generate complex graphs of entanglement correlations between the involved fields and establish mapping between the resource and complex networks of physical interactions .
Contact us (valentina.parigi@lkb.upmc.fr) for more information
Available Postdoc positions !
Experimental setups and Protocols
Experimental setups
-
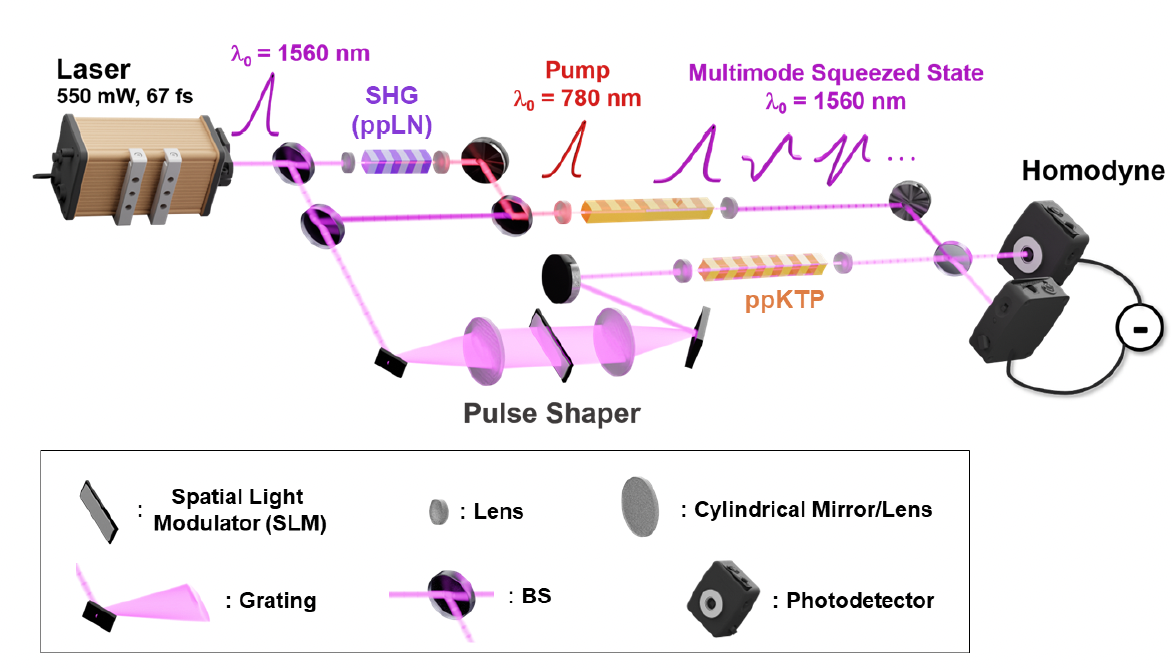
Spectrally shaped and pulse-by-pulse multiplexed multimode squeezed states of light
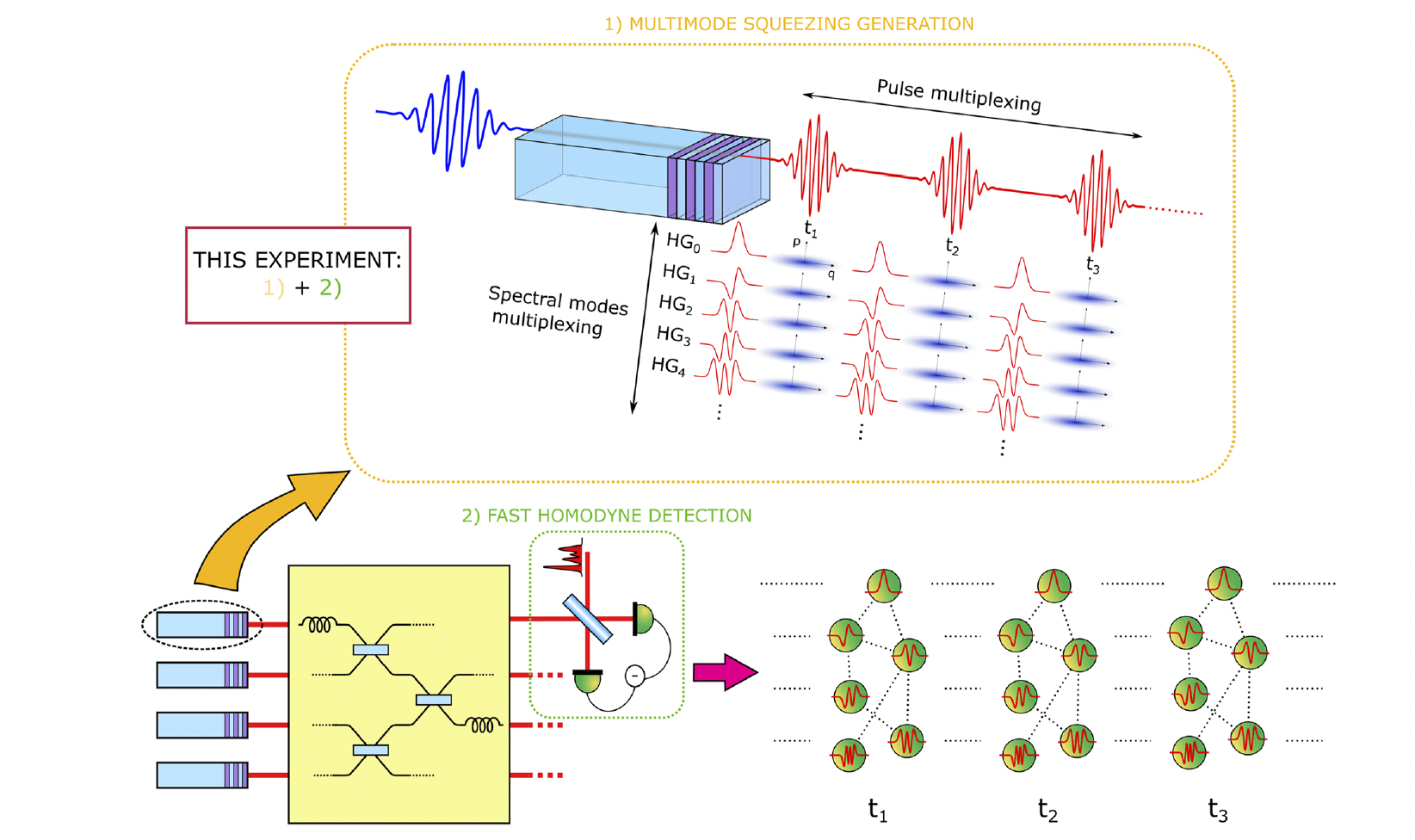
Tiphaine Kouadou, Francesca Sansavini, Matthieu Ansquer, Johan Henaff, Nicolas Treps, Valentina Parigi APL Photonics 8, 086113 (2023)
We demonstrate the simultaneous generation of 21 squeezed spectral modes at 156 MHz. We exploit the full repetition rate and the ultrafast shaping of a femtosecond light source to combine, for the first time, frequency- and time- multiplexing in multimode squeezing.
-
Multimode Squeezed State for Reconfigurable Quantum Networks at Telecommunication Wavelengths
Victor Roman-Rodriguez, David Fainsin, Guilherme L. Zanin, Nicolas Treps, Eleni Diamanti, Valentina Parigi arXiv:2306.07267 (2023) Experimental source of multimode squeezed states of light at telecommunication wavelengths. Generation at such wavelengths is especially important as it can enable quantum information processing, communication, and sensing beyond the laboratory scale. We measured significant squeezing in more than 21 frequency modes, with a maximum squeezing value exceeding 2.5 dB. We demonstrate multiparty entanglement by measuring the state’s covariance matrix. Finally, we show the source reconfigurability by preparing few-node cluster states and measure their nullifier squeezing level.
Non-Gaussian CV quantum states
-
Network structures in quantum states
M. Walschaers, N. Treps, B. Sundar, L. D. Carr, V. Parigi Emergent complex quantum networks in continuous-variables non-Gaussian states, Quantum Sci. Technol. 8 035009 (2023) or arXiv 2012.15608
 We use complex network theory to study a class of photonic continuous variable quantum states that present both multipartite entanglement and non-Gaussian statistics. We consider the intermediate scale of several dozens of modes at which such systems are already hard to characterize. In particular, the states are built from an initial imprinted cluster state created via Gaussian entangling operations according to a complex network structure. We then engender non-Gaussian statistics via multiple photon subtraction operations acting on a single node. We replicate in the quantum regime some of the models that mimic real-world complex networks in order to test their structural properties under local operations. We go beyond the already known single-mode effects, by studying the emergent network of photon-number correlations via complex networks measures. We analytically prove that the imprinted network structure defines a vicinity of nodes, at a distance of four steps from the photon-subtracted node, in which the emergent network changes due to photon subtraction. We show numerically that the emergent structure is greatly influenced by the structure of the imprinted network. Indeed, while the mean and the variance of the degree and clustering distribution of the emergent network always increase, the higher moments of the distributions are governed by the specific structure of the imprinted network. Finally, we show that the behaviour of nearest neighbours of the subtraction node depends on how they are connected to each other in the imprinted structure..
We use complex network theory to study a class of photonic continuous variable quantum states that present both multipartite entanglement and non-Gaussian statistics. We consider the intermediate scale of several dozens of modes at which such systems are already hard to characterize. In particular, the states are built from an initial imprinted cluster state created via Gaussian entangling operations according to a complex network structure. We then engender non-Gaussian statistics via multiple photon subtraction operations acting on a single node. We replicate in the quantum regime some of the models that mimic real-world complex networks in order to test their structural properties under local operations. We go beyond the already known single-mode effects, by studying the emergent network of photon-number correlations via complex networks measures. We analytically prove that the imprinted network structure defines a vicinity of nodes, at a distance of four steps from the photon-subtracted node, in which the emergent network changes due to photon subtraction. We show numerically that the emergent structure is greatly influenced by the structure of the imprinted network. Indeed, while the mean and the variance of the degree and clustering distribution of the emergent network always increase, the higher moments of the distributions are governed by the specific structure of the imprinted network. Finally, we show that the behaviour of nearest neighbours of the subtraction node depends on how they are connected to each other in the imprinted structure..
-
Mode selective single-photon addition
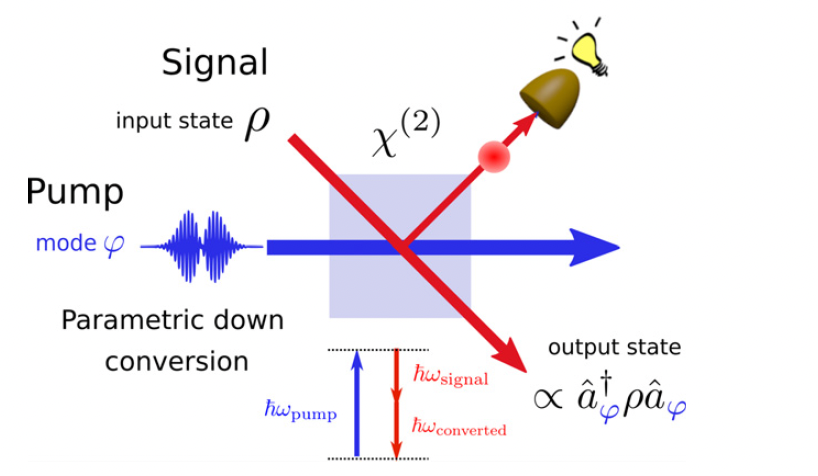
G. Roeland, S. Kaali, V. Roman Rodriguez, N. Treps, V. Parigi, Mode-selective single-photon addition to a multimode quantum field, New Journal of Physics 24 (4), 043031 (2022)
Spectro-temporal modes of light can be exploited for the generation of high-dimensional Gaussian quantum states. Such states are at the basis of continuous variable quantum information protocols where they have to support mode-selective non-Gaussian operations. We develop a general framework for single-photon addition on multimode states of light via parametric down conversion (PDC) processes. We identify the analytical conditions for single-mode and mode-selective photon addition. We show that spectral mode selectivity can be achieved in the type-II collinear down conversion, while single-mode condition are retrieved for noncollinear type-I and type-II processes. Numerical results are shown for photon addition in PDC process at near-infrared and telecommunications wavelengths.
-
Neural networks for Wigner negativity
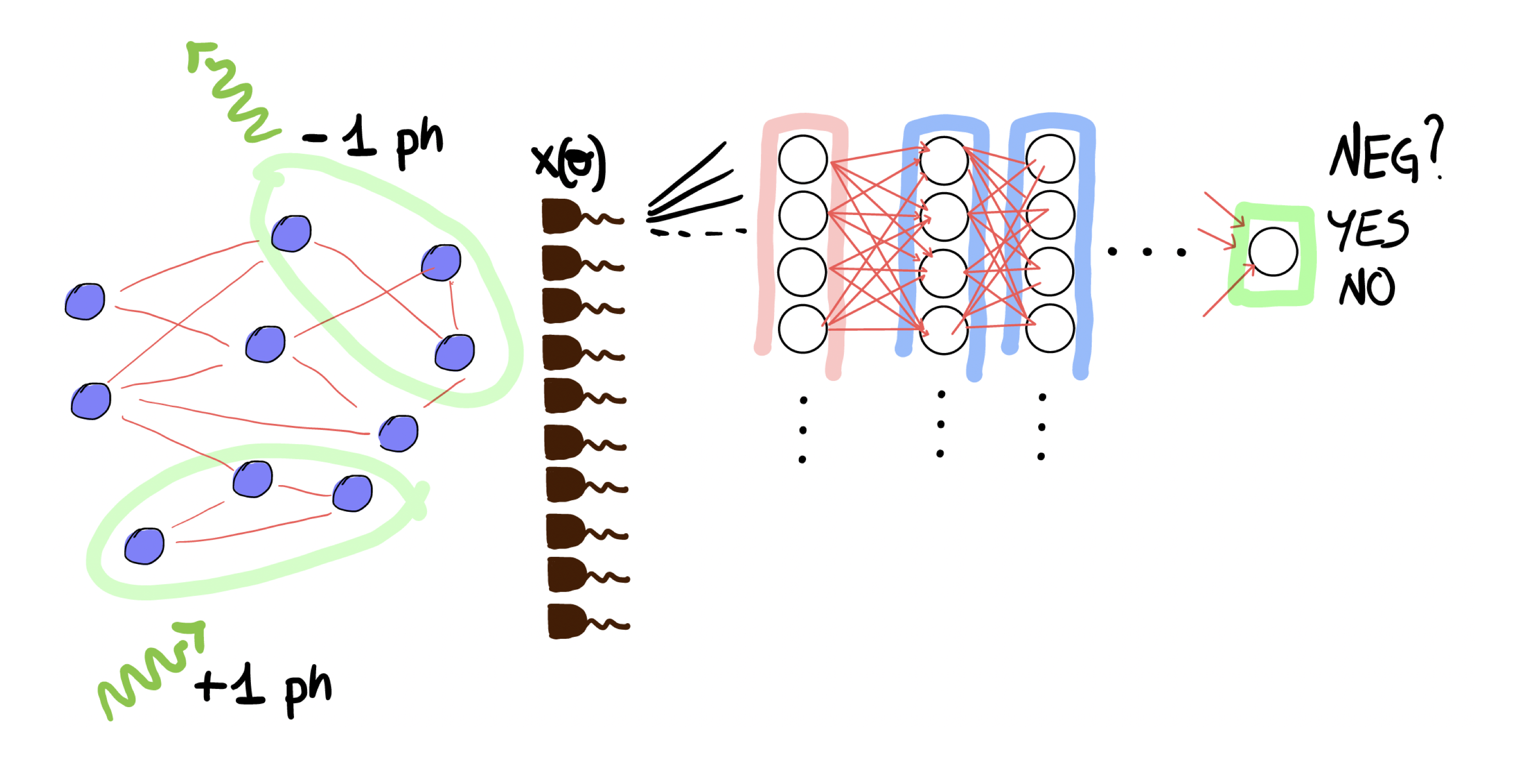
V. Cimini, M. Barbieri, N. Treps, M. Walschaers, and V. Parigi, Neural Networks for Detecting Multimode Wigner Negativity, Phys. Rev. Lett. 125, 160504 (2020) or arXiv 2003.03343We introduce a technique, based on a machine learning protocol with artificial Neural Networks, that allows to directly detect negativity of the Wigner function for multimode quantum states. We test the procedure on a whole class of numerically simulated multimode quantum states for which the Wigner function is known analytically. We demonstrate that the method is fast, accurate and more robust than conventional methods when limited amounts of data are available. Moreover the method is applied to an experimental multimode quantum state, for which an additional test of resilience to losses is carried out.
Quantum communications/information protocols

Internet is a physical complex network characterized by a scale-free structure which has been investigated to be resilient to external attacks [Goh02] Quantum communication will be delivered in networks, and part of quantum information protocols too. We investigate which complex shapes of networks will be the most effective in quantum technologies. In particular we are interested in CV cluster states, a particular kind of multipartite entangled states, shaped as complex networks. In the Continuos Variable regime it is easy to produce large entangled network. You may ask, given finite realistic resources, what are the best networks we can build in term of errors and computational noise for quantum information protocols.
-
Routing in CV quantum networks
Federico Centrone, Frederic Grosshans, and Valentina Parigi Cost and routing of continuous-variable quantum networks, Phys. Rev. A 108, 042615 (2023) , or arXiv 2108.08176 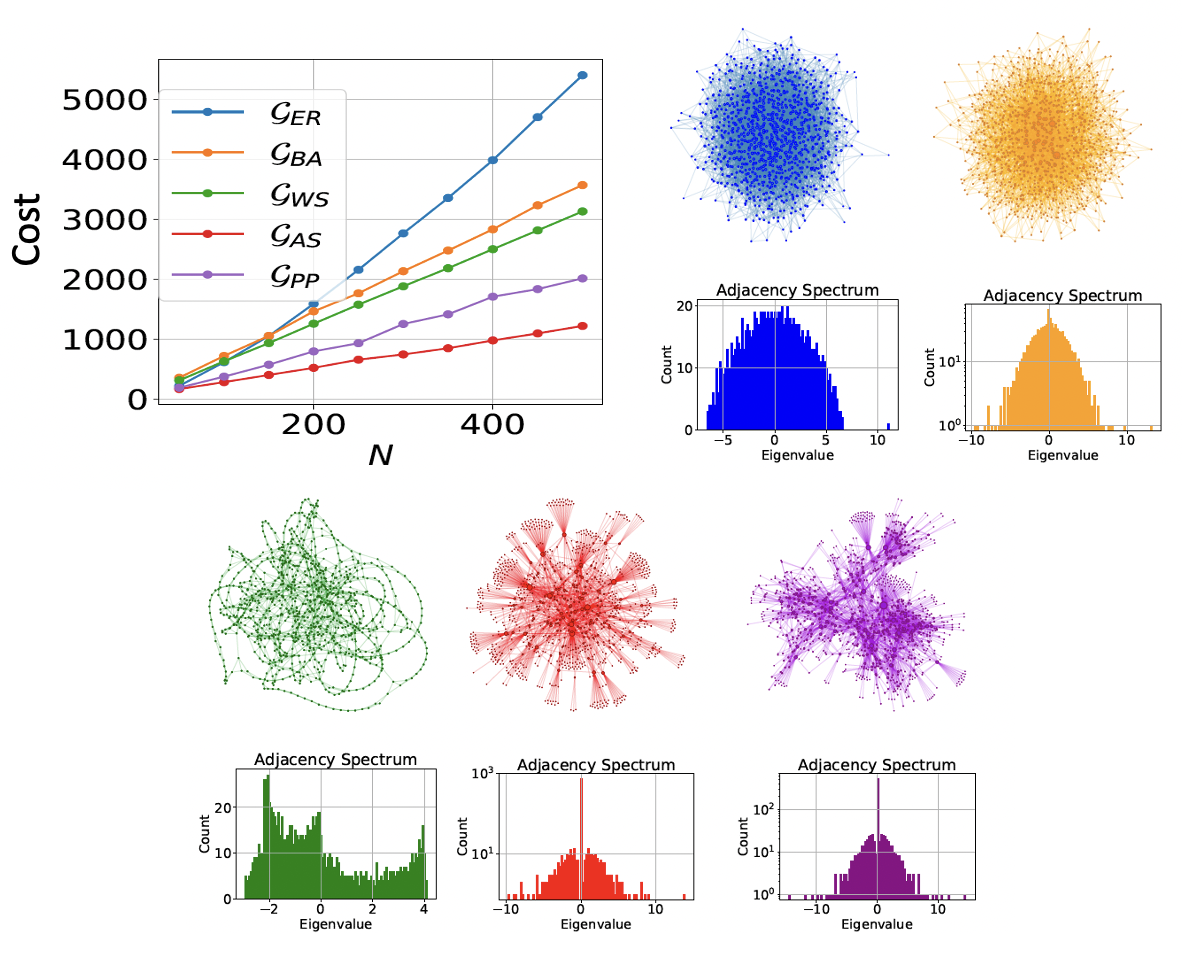
We study continuous-variable graph states with regular and complex network shapes and we report for their cost as a global measure of s queezing and number of squeezed modes that are necessary to build the network. We provide an analytical formula to compute the experimental resources required to implement the graph states and we use it to show that the scaling of the squeezing cost with the size of the network strictly depends on its topology.
We show that homodyne measurements along parallel paths between two nodes allow to increase the final entanglement in these nodes and we use this effect to boost the efficiency of an entangle ment routing protocol. The devised routing protocol is particularly efficient in running-time for complex sparse networks
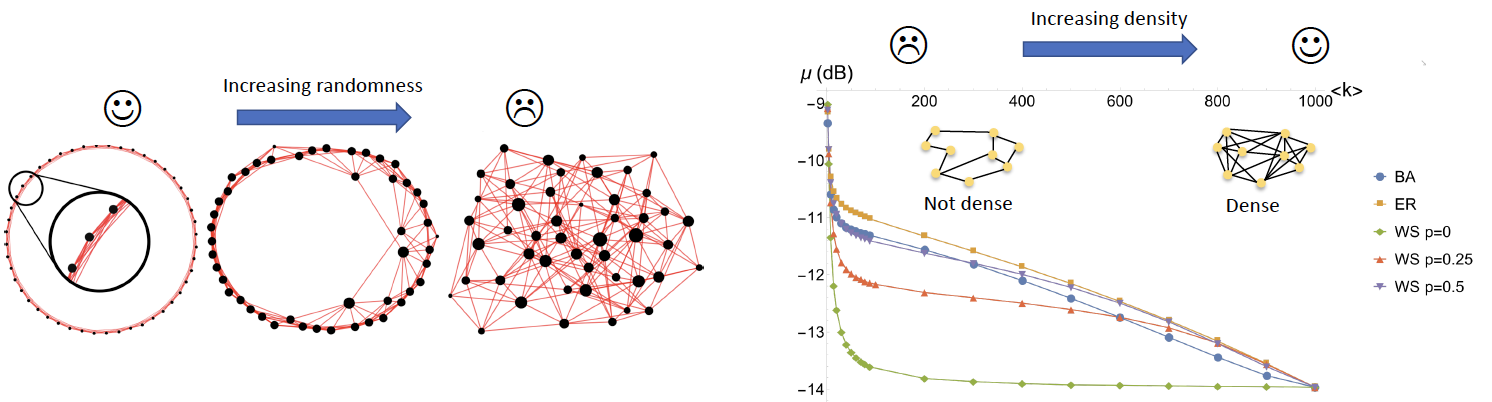 F. Sansavini and V. Parigi, Continuous Variables Graph States Shaped as Complex Networks: Optimization and Manipulation, Entropy 22, 26 (2020) Ou r graphs are built from a fixed number of (finitely) squeezed modes and linear optics transformations, which are optimize to give the best nullifiers. We found that DENSER and LESS RANDOM graphs give the best results!
F. Sansavini and V. Parigi, Continuous Variables Graph States Shaped as Complex Networks: Optimization and Manipulation, Entropy 22, 26 (2020) Ou r graphs are built from a fixed number of (finitely) squeezed modes and linear optics transformations, which are optimize to give the best nullifiers. We found that DENSER and LESS RANDOM graphs give the best results! 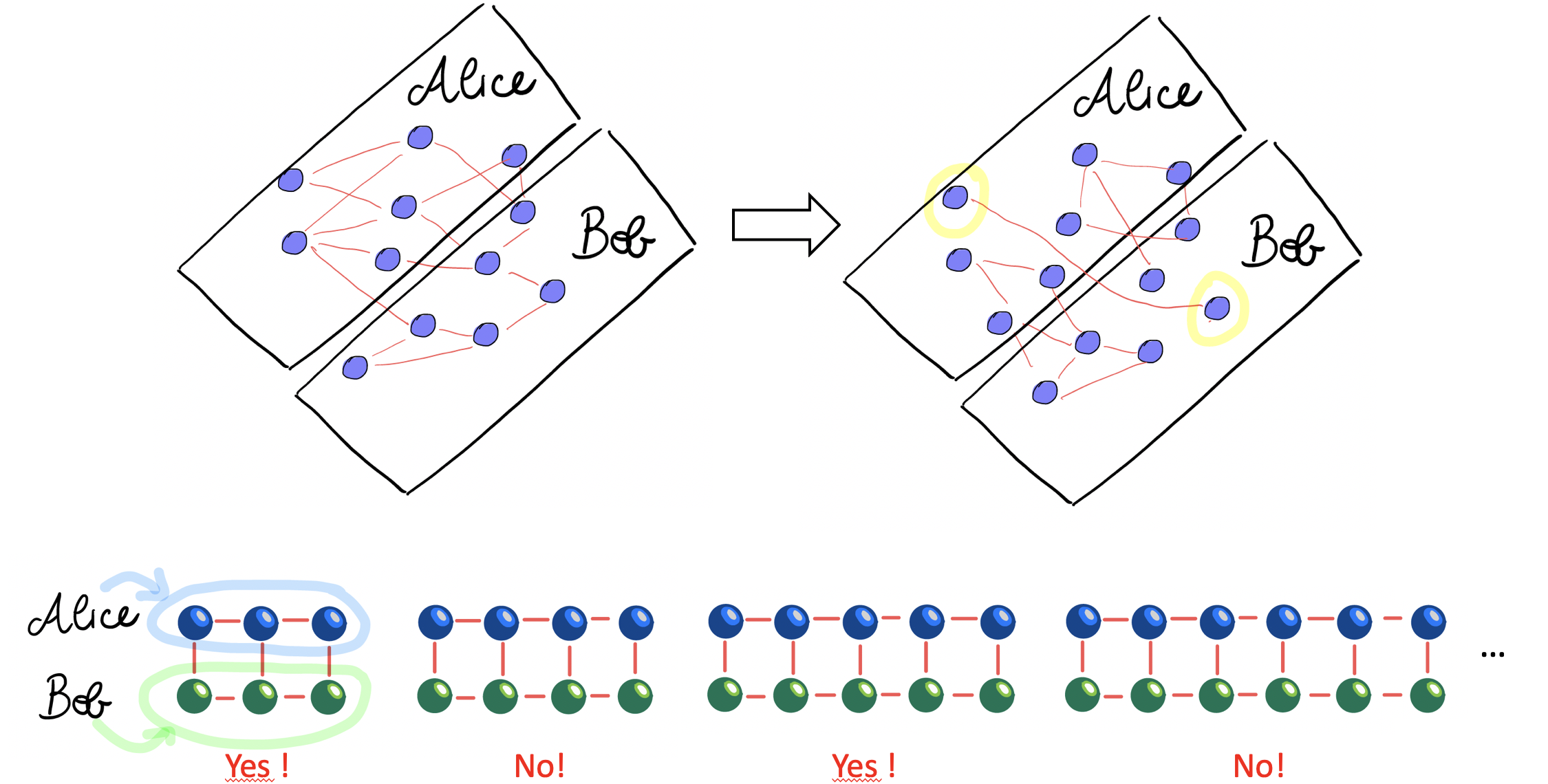
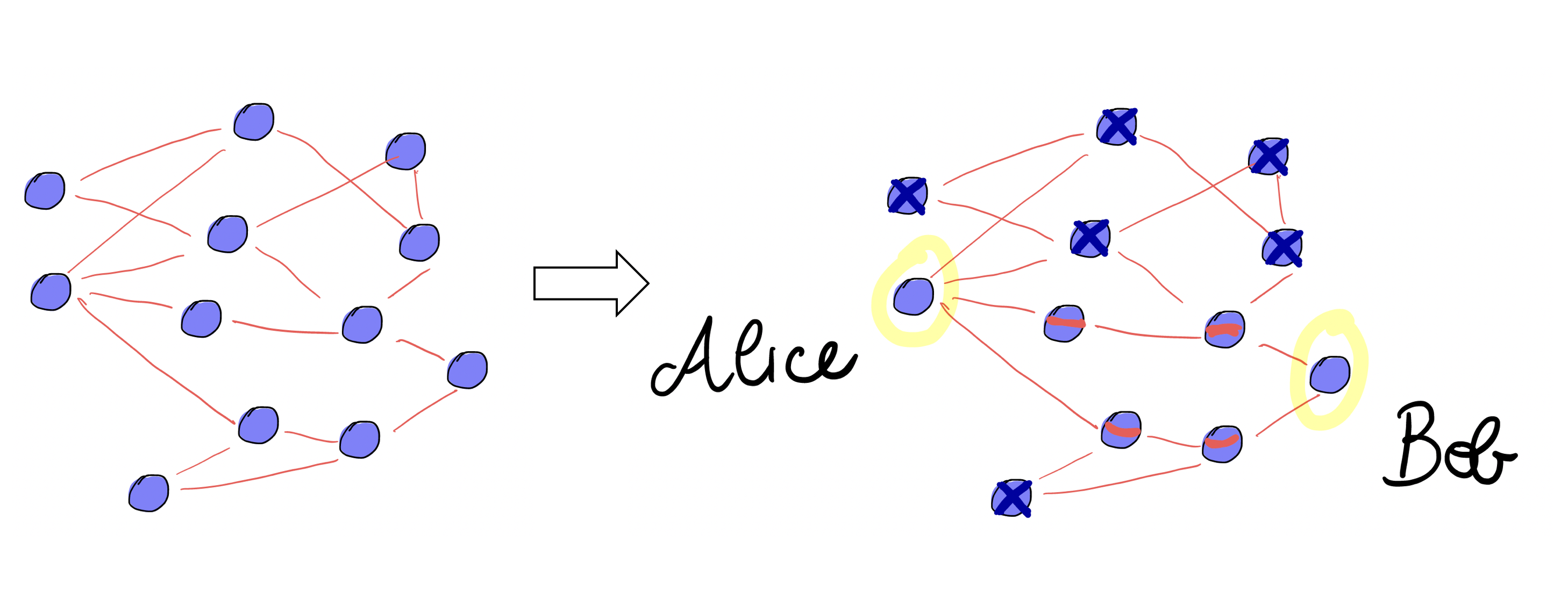
Quantum routing: Imagine that a graph structure is shared between Alice and Bob and they want to reshape the entanglement connections to create a teleportation channel between two chosen nodes. They also want to perform the protocol only vi a linear optics operations on their nodes. It turns out that, even for simple structures like grids, results are not trivial: given a fixed amount of squeezing for the initial n
odes (10 dB in this case) it is not always possible to create quantum channels between given nodes of the two parties. Moreover, it seems that grids with node number that is twice an odd number have solutions, while it is not the case for grids with node number that is twice an even number.
-
Quantum optical reservoir computing
J Henaff, M Ansquer, MC Soriano, R Zambrini, N Treps, V Parigi Optical phase encoding in pulsed approach to reservoir computing arXiv:2401.14073 (2023). The exploitation of the full structure of multimode light fields enables compelling capabilities in many fields including classical and quantum information science. We exploit data-encoding on the optical phase of the pulses of a femtosecond laser source for a photonic implementation of a reservoir computing protocol. Rather than intensity detection, data-reading is done via homodyne detection that accesses combinations of amplitude and phase of the field. Numerical and experimental results on NARMA tasks and laser dynamic predictions are shown. We discuss perspectives for quantum enhanced protocols.
J. Nokkala, R. Martínez-Peña, G. L. Giorgi, V. Parigi, M. C Soriano, R. Zambrini, Gaussian states of continuous-variable quantum systems provide universal and versatile reservoir computing, Communications Physics volume 4, Article number: 53 (2021) Quantum reservoir computing aims at harnessing the rich dynamics of quantum systems for machine-learning purposes. It can be used for online time series processing while having a remarkably low training cost. Here, we establish the potential of continuous-variable Gaussian states of linear dynamical systems for quantum reservoir computing. We prove that Gaussian resources are enough for universal reservoir computing. We find that encoding the input into Gaussian states is both a source and a means to tune the nonlinearity of the overall input-output map. We further show that the full potential of the proposed model can be reached by encoding to quantum fluctuations, such as squeezed vacuum, instead of classical fields or thermal fluctuations. Our results introduce a research paradigm for reservoir computing harnessing quantum systems and engineered Gaussian quantum states.
Look at other results of our collaborators at IFISC !
Simulation of structured quantum environment
P. Renault, J. Nokkala, G. Roeland , N. Y. Joly R. Zambrini, S. Maniscalco, J. Piilo N. Treps, V. Parigi, Experimental optical simulator of reconfigurable and complex quantum environment, PRX Quantum 4, 040310 (2023)
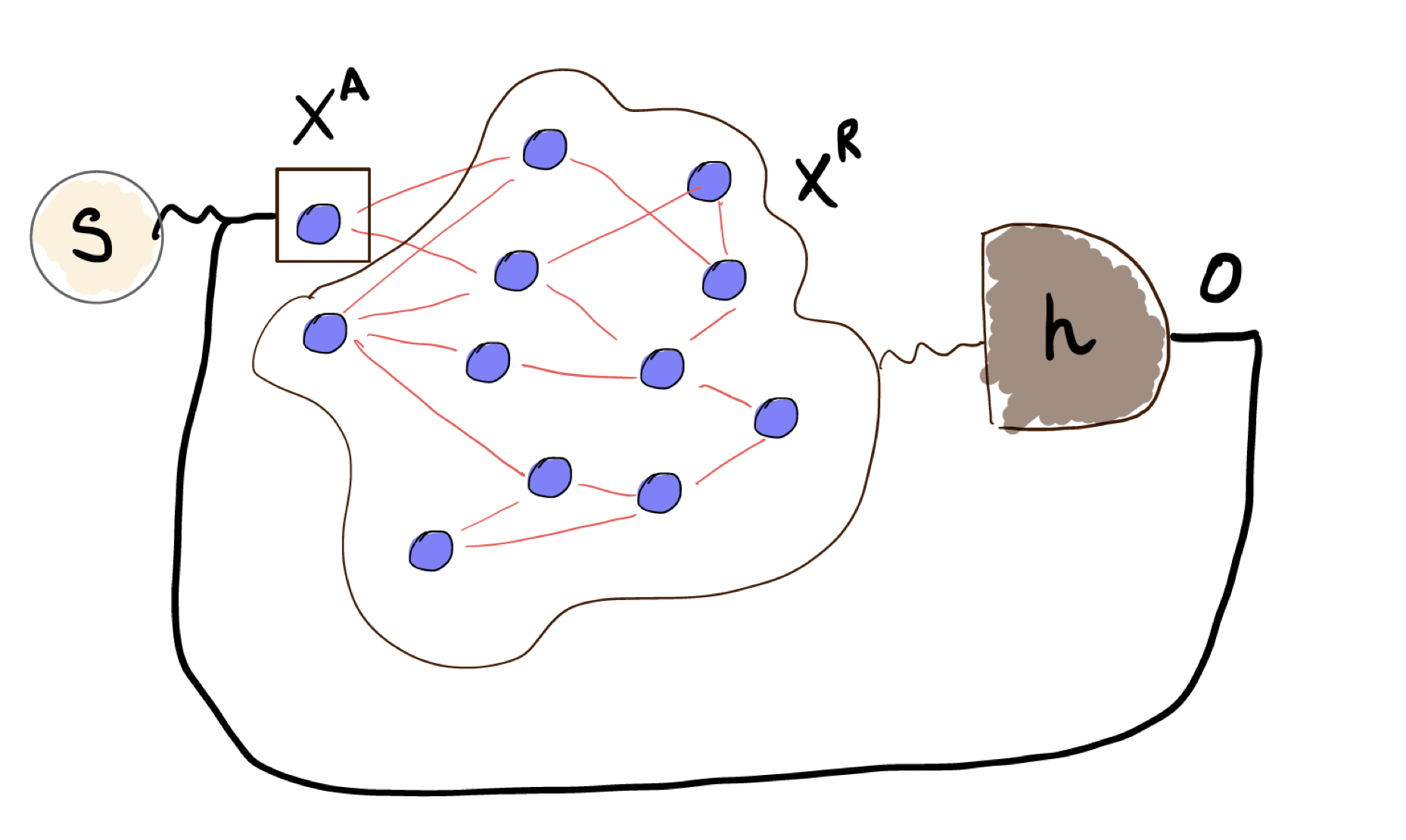
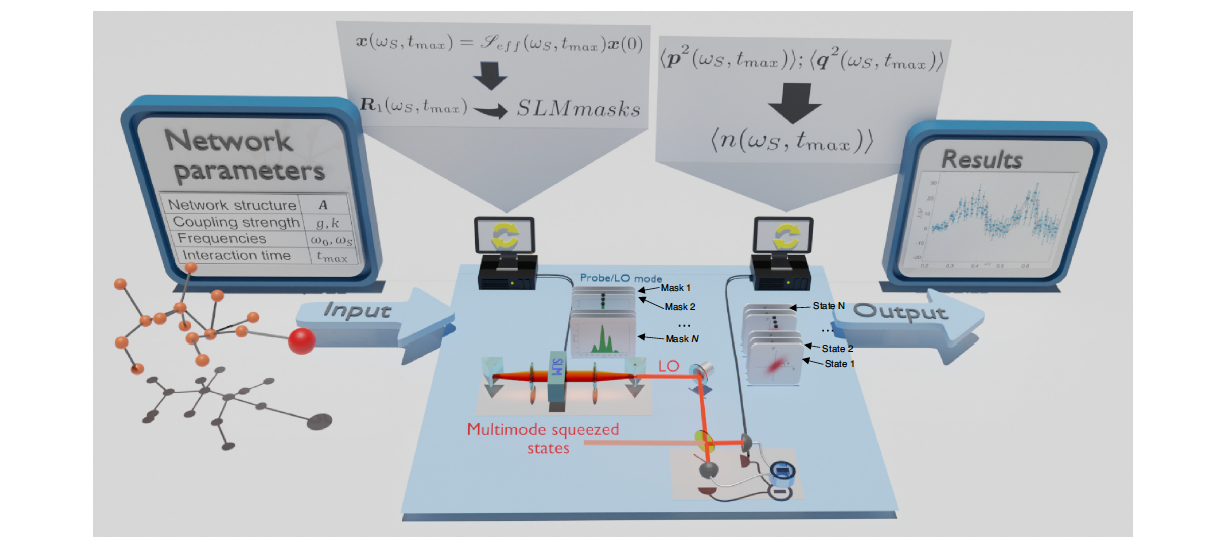 No quantum system can be considered totally isolated from its environment. In most cases the interaction between the system of interest and the external degrees of freedom deeply changes its dynamics, as described by open quantum system theory. Nevertheless engineered environment can be turned into beneficial effects for some quantum information tasks. Here we demonstrate an optical simulator of a quantum system coupled to an arbitrary and reconfigurable environment built as a complex network of quantum interacting systems. We experimentally retrieve typical features of open quantum system dynamics like the spectral density and quantum non-Markovianity, by exploiting squeezing and entanglement correlation of a continuous-variable optical platform. This opens the way to the experimental tests of open quantum systems in reconfigurable environments that are relevant in, among others, quantum information, quantum hermodynamics, quantum transport, and quantum synchronization.
No quantum system can be considered totally isolated from its environment. In most cases the interaction between the system of interest and the external degrees of freedom deeply changes its dynamics, as described by open quantum system theory. Nevertheless engineered environment can be turned into beneficial effects for some quantum information tasks. Here we demonstrate an optical simulator of a quantum system coupled to an arbitrary and reconfigurable environment built as a complex network of quantum interacting systems. We experimentally retrieve typical features of open quantum system dynamics like the spectral density and quantum non-Markovianity, by exploiting squeezing and entanglement correlation of a continuous-variable optical platform. This opens the way to the experimental tests of open quantum systems in reconfigurable environments that are relevant in, among others, quantum information, quantum hermodynamics, quantum transport, and quantum synchronization.
Other publications and references
-
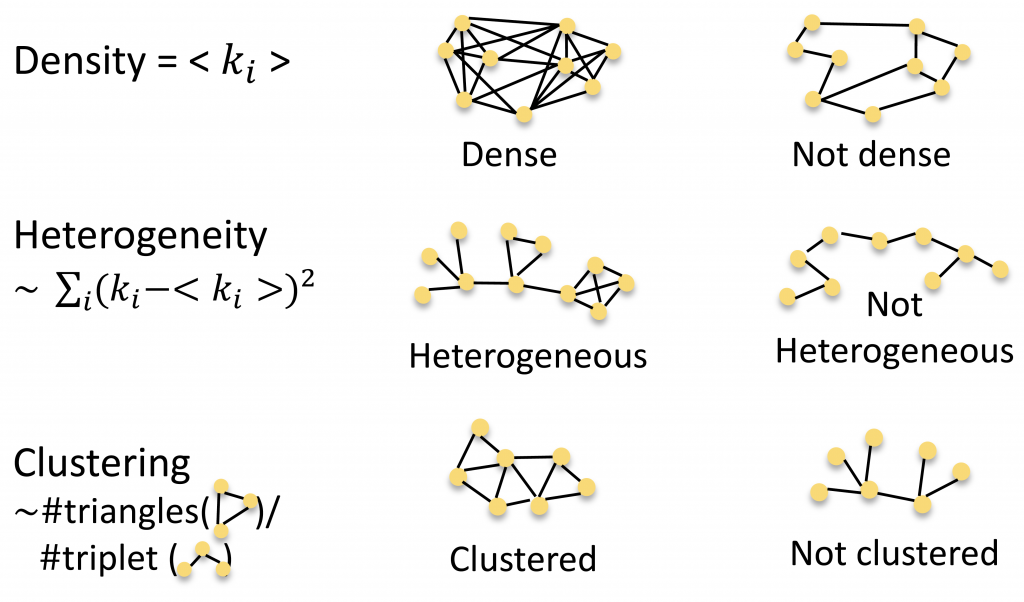
Complex networks: Networks are physical structures represented by graph: they are composed by (nodes) connected via links (edges), which depict physical interactions or correlations. They are often classified via the probability distributions of their edges per node (= degree), which reflects the way they grow and which is strongly connected with their global behavior (dynamics) and functionalities (resilience under errors and failures)
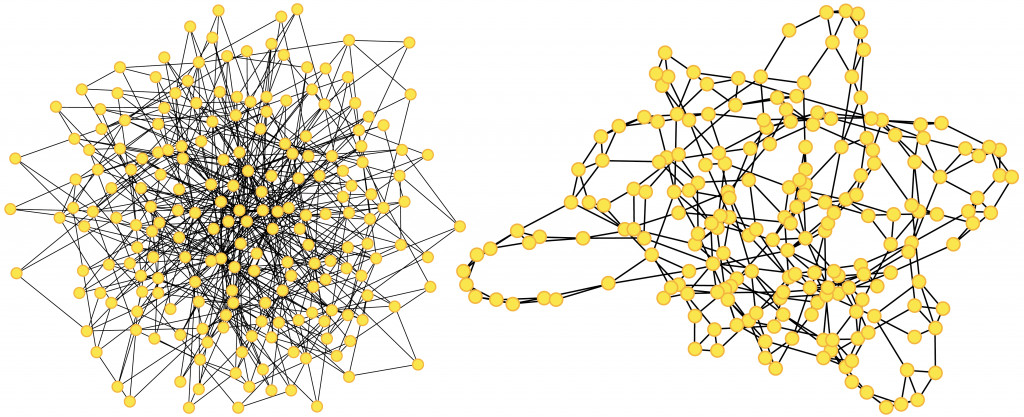
Left: Barabasi -Albert (B.-A.) graph of 200 nodes. The more connected a node is, the more likely it is to receive new links. B.-A. networks are characterized by power law distributions of links per node, which are typical of many real-world networks. Right: Watt-Strogatz graph of 200 nodes: it is built from a regular ring lattice, where each node is symmetrically connected to a fixed portion of the neighbours, then connections are rewired it with a given probability.
In the last twenty years network theory has provided a deep insight of complex systems, assembling theoretical tools able to the describe dynamical behaviour of biological, social and technological structures. During the recent years a new area applying network theory and complex networks to quantum physical systems has emerged
Other publications and references
- [Sun21] B. Sundar, M. Walschaers, V. Parigi and L. D Carr, Response of quantum spin networks to attacks, J. Phys. Complex. 2 035008 (2021)
-
[Rom21] V. Roman-Rodriguez, B. Brecht, S. Kaali, C. Silberhorn, N. Treps, E. Diamanti, V. Parigi, Continuous variable multimode quantum states via symmetric group velocity matching, New J. Phys. 23 043012 (2021)
-
[LaVo20]L. La Volpe, S. De, T. Kouadou, D. Horoshko, M. I. Kolobov, C. Fabre, V. Parigi, and N. Treps, Multimode single-pass spatio-temporal squeezing, Optics Express, Vol.28 pp 12385-12394 (2020)
- [Nok18] Nokkala, F. Arzani, F. Galve, R. Zambrini, S. Maniscalco, J. Piilo, N. Treps, V. Parigi, Reconfigurable optical implementation of quantum complex networks, New J. Phys. 20, 053024 (2018)
-
[Nok17] J. Nokkala, S. Maniscalco and J.Piilo Open Systems & Information Dynamics Vol. 24, No. 04, 1740018 (2017)
- [Nok18] J. Nokkala, F. Arzani, F. Galve, R. Zambrini, S. Maniscalco, J. Piilo, N. Treps, V. Parigi, Reconfigurable optical implementation of quantum complex networks, New J. Phys. 20, 053024 (2018)
- [Gao16] J.Gao, B. Barzel, A.L. Barabási, Nature 530, 307 (2016)
- [Val17] M. A. Valdez, D. Jaschke, D. L. Vargas, and L. D. Carr Physical Review Letters 119, 225301 (2017)).
- [Goh02] K-Il Goh et al. PNAS 99, 12583, (2002).