QUANTUM CHAOS
Quantum kicked rotors, Dynamical localizationPublications
- [1] J. Ringot et al., Experimental Evidence of Dynamical Localization and Delocalization in a Quasiperiodic Driven System, Phys. Rev. Lett. 85, 2741 (2000)
- [2] P. Szriftgiser et al., Observation of Sub-Fourier Resonances in a Quantum-Chaotic System, Phys. Rev. Lett. 89, 224101 (2002)
- [3] H. Lignier et al., Reversible destruction of dynamical localization, Phys. Rev. Lett. 95, 234101 (2005)
Dynamical localization
For a system depending periodically on time, energy is not a conserved quantity. One can thus observe — when the classical dynamics is complex and in particular chaotic — an average increase of the energy of a system proportional to time, that is to say a situation of chaotic, deterministic, diffusive motion.

A known example is the kicked rotor. The same system, when its evolution is governed by quantum mechanics, can show up a different behavior, namely a freezing of the diffusive motion (called dynamical localization) because of destructive interference. By subjecting cold atoms to time-dependent laser beams, it is possible to study this problem experimentally, as well as the transition from the quantum to the classical regime.
This experiment has been carried out by the team of J. C. Garreau and P. Szriftgiser (quantum chaos group of the PhLAM lab). Furthermore, we have shown how dynamical localization could be destroyed when the system is excited quasi-periodically instead of periodically, which is connected with the question of the dependence of Anderson localization on the number of degrees of freedom of the system [1]. We have shown that the quantum chaotic system exhibits an extraordinary sensitivity to the periodic or quasi-periodic character of the excitation, which allows to observe resonance lines much sharper than the limit set by the Fourier inequality, but also to cross in a controlled and reversible way over a situation of diffusion to a situation of localization [2,3]. This opens interesting perspectives for the field of coherent control of the internal state of a quantum system.
Publications
- [1] J. Chabé et al., Experimental Observation of the Anderson Metal-Insulator Transition with Atomic Matter Waves, Phys. Rev. Lett. 101, 255702 (2008)
- [2] M. Lopez et al., Phase diagram of the Anderson transition with atomic matter waves, New J. Phys. 15, 065013 (2013)
- [3] M. Lopez et al., Experimental Test of Universality of the Anderson Transition, Phys. Rev. Lett. 108, 095701 (2012)
Anderson transition and quantum chaos
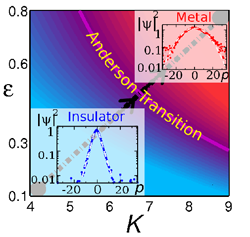 An important problem studied by the team is the Anderson metal-insulator transition with cold atoms. The Anderson transition is a quantum phase transition between a metallic state and an insulating state. In condensed matter systems, the localization phenomenon is hard to detect because interactions between electrons are important and disorder is impossible to control with high accuracy. On the contrary, cold atoms allow for a better control of parameters and can be used to realize a single-body problem. In this context, the team studies the Anderson transition by using a system of the field of quantum chaos which belongs to the same universality class as the Anderson model. This system, called pseudo-periodic kicked rotor, is simpler to realize experimentally and simpler to study theoretically than the true three-dimensional problem.
An important problem studied by the team is the Anderson metal-insulator transition with cold atoms. The Anderson transition is a quantum phase transition between a metallic state and an insulating state. In condensed matter systems, the localization phenomenon is hard to detect because interactions between electrons are important and disorder is impossible to control with high accuracy. On the contrary, cold atoms allow for a better control of parameters and can be used to realize a single-body problem. In this context, the team studies the Anderson transition by using a system of the field of quantum chaos which belongs to the same universality class as the Anderson model. This system, called pseudo-periodic kicked rotor, is simpler to realize experimentally and simpler to study theoretically than the true three-dimensional problem.
In this field, an important achievement of the team, in collaboration with the quantum chaos group of the PhLAM lab in Lille, was to numerically and experimentally determine the critical exponent of the transition with the kicked rotor [1]. Recenty, the phase diagram of the pseudo-periodic kicked rotor has been explored [2] and the universality of the critical exponent has been tested with respect to the microscopic details of the model [3]. Presently our research more specifically deals with the study of wave-function fluctuations at the transition in the kicked-rotor model, with special interest in the multifractal properties of the wave functions.
