QFL - Quantum Fluids of Light Team
Superfluidity of light : from Quantum Optics to Quantum Simulation.TEAM MEMBERS
PERMANENT STAFF
- Quentin Glorieux
- Alberto Bramati
- Elisabeth Giacobino
POSTDOC
- Simon Pigeon
- Tom Bienaimé
PHD STUDENT
- Quentin Fontaine
- Anne Maitre
- Murad Abuzarli
- Huiqin Hu
What is a Quantum Fluid of Light ?

QUANTUM FLUID OF LIGHT.
Credit : Maxime Richard
Quantum Hydrodynamics
Quantum fluids Physics is the study of hydrodynamic systems which demonstrate a quantum behavior. A large range of many-particle systems are currently under intense investigation, from liquid Helium to electrons in solids, to quark-gluon plasma and trapped gases of ultra-cold atoms. Surprisingly, these very different systems show similar behavior when the thermal de Broglie wavelength becomes comparable or larger than the average inter-particle spacing. In this regime, the Bose versus Fermi statistics of the particules starts playing a critical role in determining the properties of the fluid. For exemple, non-interacting fermions will exhibit Fermi pressure down to zero temperature thanks to the rigidity of the Fermi sphere, while in a non-interacting Bose gas a macroscopic fraction of the particules will ac- cumulates in the lowest-energy state, leading to a Bose-Einstein condensate.
When interactions between particules are not negligible, physics become even more fascinating with purely quantum effects fading in, like superconductivity, superfluidity and the fractional quantum Hall effect.
Quantum fluids of light – QFL
Historically, this area of research (theoretical and experimental) deals with massive material particules (atoms, electrons…). However, we know since the early days of quantum mechanics, that photons in a box can be interpreted as a massless Bose gas of non-interacting particules. This fruitful interpretation leads for example to the correct black-body radiation spectrum. Recently, it has been realized that under suitable circumstances photons can acquire an effective mass and will behave as a quantum fluid of light with photon-photon interactions.
Our research group have shown experimental demonstrations of superfluidity and other quantum hydrodynamical effects such as quantized vortices and solitons in a confined geometry using semi-conductor planar micro-cavities.
NEW : Click Here for a 3D lab tour !!
The QFL Team works on 3 main project :
-
QFL: Quantum Dynamics of exciton-polaritons condensates
-
Q-FLAME: Superfluidity of light in atomic vapor
-
C-Flight : Theory of correlated fluid of light – Hydrodynamic and Thermodynamic aspects
A short tutorial on Exciton-Polaritons
Exciton-Polaritons
The de Broglie wavelength of a particle is defined as h/p, with h the Planck constant and p the particle momentum.For an assembly of identical particles, when the de Broglie wavelength becomes comparable or larger than the average interparticle spacing, it is possible to observe Bose-Einstein or Fermi-Dirac statistics of the constituent particles.
For example, in a Bose gas, a macroscopic fraction of the particles can accumulate in the lowest energy state and give rise to the so-called Bose-Einstein condensate (BEC).
When this property of quantum degeneracy is combined with inter-particle interactions, a quantum gas becomes a quantum fluid and produce a variety of spectacular effects such as superfluidity.
Exciton-polaritons microcavity is a very attractive system to explore the physics of quantum hydrodynamics.
What is a polariton ?
Generally speaking, polaritons are quasi-particules arising from the strong coupling between an electromagnetic field and a dipolar transition. A dipolar transition is characterized by its ability to absorb and emit photons at a well-defined energy. When an electromagnetic mode at the same energy is coupled to this transition, we observe a splitting of the energy states for the coupled system. This can be understood intuitively as a dressed-state of the emitter by the electromagnetic field. We name these dressed states : upper and lower polaritons (respectively UP and LP).
Different types of polaritons.
We have just seen than the definition of polaritons can apply to a large variety of physical systems. In our group we are studying two types of polaritons : exciton-polaritons and atomic-polaritons. Exciton-polaritons are polaritons with an excitonic-transition as the emitter. Let us recall that an exciton is a bound-state between an electron and a hole, which can be observed, for example, in a semiconductor quantum well. For the experiments conducted in our lab, we use semiconductor structures of GaAs-AlGaAs and GaAs-InGaAs grown by molecular beam epitaxy at LPN (Marcoussis) and EPFL (Lausanne). To really create a polariton, this quantum well has to be placed inside a photonic cavity, and this is by growing a Bragg mirror structure around the quantum well.
Research project : QFL
Quantum Dynamics of exciton-polaritons condensatesRecent publications
- T. Boulier, E. Cancellieri, N. Sangouard, Q. Glorieux, A. Kavokin, D Whittaker, E. Giacobino and A. Bramati, Injection of Orbital Angular Momentum and Storage of Quantized Vortices in Polariton Superfluids. Phys. Rev. Lett. 116, 116402 (2016)
- T. Boulier, H. Terças, D. D. Solnyshkov, Q. Glorieux, E. Giacobino, G. Malpuech and A. Bramati, Vortex Chain in a Resonantly Pumped Polariton Superfluid. Scientific Reports, 5, 9230 (2015)
- T. Boulier, M. Bamba, A. Amo, C. Adrados, A. Lemaître, E. Galopin, I. Sagnes, J. Bloch, C. Ciuti, E. Giacobino and A. Bramati, Polariton-generated intensity Squeezing in semiconductor micropillars, Nature Communications, 5, 3260 (2014).
- R. Hivet, H. Flayac, D. Solnyskhov, D. Tanese, T. Boulier, D. Andreoli, J. Bloch, E. Giacobino, A. Kavokin, A. Bramati, G. Malpuech, A. Amo, Half-Solitons in a polariton quantum fluid behave like magnetic monopoles. Nature Physics 8, 724 (2012).
- C. Adrados, T. C. H. Liew, A. Amo, M. D. Martín, D. Sanvitto, C. Antón, E. Giacobino, A. Kavokin, A. Bramati and L. Viña, Motion of Spin Polariton Bullets in Semiconductor Microcavities. Phys. Rev. Lett. 107, 146402 (2011).
- D. Sanvitto, S. Pigeon, A. Amo, D. Ballarini, M. De Giorgi, I. Carusotto, R. Hivet, F. Pisanello, V. G. Sala, P. S. S. Guimaraes, R. Houdré, E. Giacobino, C. Ciuti, A. Bramati & G. Gigli, All-optical control of the Quantum flow of a polariton condensate. Nature Photonics, 5, 610 (2011).
- A. Amo, S. Pigeon, D. Sanvitto, V.G. Sala, R. Hivet, I. Carusotto, F. Pisanello, G. Leménager, R. Houdré, E. Giacobino, C. Ciuti & A. Bramati, Polariton Superfluids reveal Quantum Hydrodynamical Solitons. Science, 332, 1167 (2011).
Superfluidity and Cerenkov effect
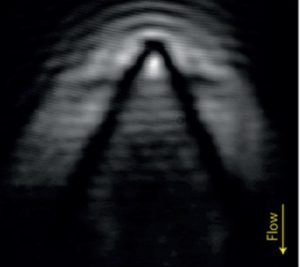 During the last years, we have studied the superfluid regime of exciton-polaritons in microcavities, and we have evidenced the superfluidity of a polaritonic fluid created by laser excitation. Superfluidity can be characterized by the flow without friction around a potential barrier. In our system (semiconductor microcavity),the polariton fluid is confined in the plane of the quantum well and can be created with a given momentum and density thanks to the excitation laser angle and power respectively and the potential barriers can be a local defect in the cavity growth, or an externally controlled perturbation such as a population of exciton locally created via optical excitation. By modifying the laser power, we can probe various density regime and study the transition from a normal fluid (low density-low interactions) to a superfluid (high intensity-strong interactions). An interesting phenomena can also be evidenced by modifying the laser angle, ie the fluid velocity, is the observation of a Cerenkov cone when the fluid flows faster than the speed of sound in the fluid. These observations are in very good agreement with a generalized Gross-Pitaevskii theory and demonstrate than polaritons are a powerful system to explore the physics of out-of-equilibrium quantum fluids.
During the last years, we have studied the superfluid regime of exciton-polaritons in microcavities, and we have evidenced the superfluidity of a polaritonic fluid created by laser excitation. Superfluidity can be characterized by the flow without friction around a potential barrier. In our system (semiconductor microcavity),the polariton fluid is confined in the plane of the quantum well and can be created with a given momentum and density thanks to the excitation laser angle and power respectively and the potential barriers can be a local defect in the cavity growth, or an externally controlled perturbation such as a population of exciton locally created via optical excitation. By modifying the laser power, we can probe various density regime and study the transition from a normal fluid (low density-low interactions) to a superfluid (high intensity-strong interactions). An interesting phenomena can also be evidenced by modifying the laser angle, ie the fluid velocity, is the observation of a Cerenkov cone when the fluid flows faster than the speed of sound in the fluid. These observations are in very good agreement with a generalized Gross-Pitaevskii theory and demonstrate than polaritons are a powerful system to explore the physics of out-of-equilibrium quantum fluids.
Various other topological excitations has been demonstrated in our group in polaritons fluids such as hydrodynamic solitons, and vortices.
Currently our activities focus on the creation of artificial defects with arbitrary shapes and potentially fast dynamics comparatively to polariton lifetimes.
Topological excitations : vortices, solitons…
Vortices and solitons are the fundamental topological excitations of a quantum fluid of interacting bosons. The flexibility provided by the use of a SLM or the recently developed Q-plates (that can generate orbital angular momentum coupled with polarization in a light beam), allowing the creation, at will, of a controlled number of vortices, half vortices with defined vorticity and spin texture in a polariton condensate, offers an ideal playground for the study of these excitations.

Vortices in a polariton condensate
Polariton fluids have two spin components with very weak inter-spin interactions. They can be selectively generated by using a circularly polarised optical excitation. One can therefore create a scalar fluid with integer vortices and solitons as excitations. Another option is to resonantly excite the system with a linearly polarised light. In this case, both spin components are equally present and we deal with a spinor fluid. The topological excitations are half vortices and half solitons which tend to be spatially separated due to the effective fields. Recently, these excitations have been generated in the group and their individual properties studied from a qualitative point of view.
We are currently working on a fully quantitative understanding of the properties of the individual defects, their mutual interactions, and then to study in details their collective behaviour.
Superfluid propagation in disordered media
A very important difference between classical and quantum fluids is their interaction with potentials. Quantum fluids are characterized by extended coherence, which makes possible not only superfluidity, but also particular localization phases, such as the Anderson or weak localization.
In order to investigate these effects, we study the propagation of polariton flows in artificial disordered landscapes. The problem of the ground state of polaritons in such system and its superfluid or localized properties has already been treated theoretically, and interesting phases, such as the glassy and half- superfluid were described, but the experimental study is missing.
On the other hand, the propagation of polariton flows in such systems is very complex due to the presence of nonlinearities. The disorder can be created and controlled illuminating the sample with a random speckle intensity light pattern which in turn modulates in a random way the potential seen by polaritons. Increasing the average amplitude of the disorder, the transition between the superfluid and insulator regimes can be investigated.
In analogy with recent experiments performed in atomic 1D BEC, the Anderson localization regime in a 2D system will be investigated. The purely two dimensional nature of polaritons and the full control of their energy are key advantages compared to the atomic BECs, where the 2D Anderson localization is very hard to observe.
Finally we study how the disorder affects the polariton properties in systems with periodic potentials, created by applying a periodic optical potential. Periodic lattice allows to strongly increase the polariton mass and thus to explore the deep superfluid regime, where the interaction energy strongly exceeds the kinetic one.
Research project - QFLAME
Superfluidity of light in atomic vaporRecent Publications
Q. Fontaine, T. Bienaime, S. Pigeon, E. Giacobino, A. Bramati, Q. Glorieux. Observation of the Bogoliubov dispersion in a fluid of light, Phys. Rev. Lett. – Editors’ Suggestion, 121, 183604 , (2018).
Historically, research in many body-physics (theoretical and experimental) deals with massive material particules (atoms, electrons…). However, we know since the early days of quantum mechanics, that photons in a box can be interpreted as a massless Bose gas of non-interacting particules. This fruitful interpretation leads for example to the correct black-body radiation spectrum.
Recently, it has been realized that under suitable circumstances photons can acquire an effective mass and will behave as a quantum fluid of light with photon-photon interactions. The Quandyde project has allowed experimental demonstrations of superfluidity and other quantum hydrodynamical effects such as quantized vortices and solitons in a confined geometry using semi-conductor planar micro-cavities.
Building on these experiments, we propose to use a different geometry (propagating light instead of confined) to study quantum fluids of light.
Superfluidity of light in propagating geometries
An alternative to the confined geometry in cavities is to use a monochromatic light field propagating in a non-linear χ(3) medium showing an intensity dependent refractive index. Under the paraxial approximation, the transverse amplitude of the light field can be described using a striking analogy with the formalism of the Gross-Pitaevskii equation for the macroscopic wave-function of a Bose-Einstein condensate (see below).
However, an important difference must be highlighted. As the Gross-Pitaevskii equation describes the evolution of superfluid Helium order parameter in time, the non-linear wave equation for the transverse electric field refers to an evolution in space along the propagation direction.
It is therefore crucial to have in mind this space-time mapping when discussing fluids of light in the propagating geometry. As a consequence, we can study the time evolution of a 2D Bose gas in this configuration. The spatial evolution is observed in the transverse direction and the temporal evolution is mapped along the propagation axis. Simple imaging techniques give a direct access to the temporal evolution of the fluid in position and momentum space

Research project - C-Flight
Theory of correlated fluid of light - Hydrodynamic and Thermodynamic aspectsThe field of microcavity polaritons has undergone an impressive expansion in the past decade, with the discovery of polariton Bose-Einstein condensation and the demonstration of their quantum fluid properties. The high quality and mastered technology in the epitaxial fabrication of GaAs based planar semiconductor microcavities makes this system an extraordinary workbench for the study of fluid of light but also of other non-linear optical phenomena (optical bistability, optical; parametrical oscillation; etc). The advances in the realisation of ultra-high quality samples open unprecedented possibilities for unravelling novel physical effects in quantum fluids of light and for implementing disruptive polariton devices for future information and communication technology.
The C-flight project proposes to focus on the theory of two fundamental features of polariton physics.
Quantum Simulation with exciton-polaritons
The first research line is dedicated to the in-depth study of polariton fluids properties. Focusing on the spin properties and the topological excitations taking place in such fluid, we expect to provide a genuine progresses in the understanding of polariton systems tractable to other non-linear optical devices presenting similar dynamics.
Considering polariton flow for itself, we investigate two interacting quantum fluids, topological excitations taking place in superfluid, as well as Kibble-Zurek mechanism. Moreover the exact same system will be used to simulate other quantum states of matter and related outstanding phenomena such as Anderson localisation and Mott-Superfluid transition. The large number of key parameters (density, phase, effective potential landscape) readily easily accessible allows one to use polariton fluid as a quantum simulator.
Quantum Thermodynamics
The second component of the C-FLigHT project relies on recent advances in the emerging field of Quantum Thermodynamics. By studying microcavity polaritons from an innovative thermodynamics of open- quantum-systems perspective we expect to gain a finer understanding of these system dynamics. The goal is to describe thermodynamic phenomenon and to explore universal mechanism such as Kibble-Zurek mechanism in the general context of quantum optics and solid-state physics using polariton devices as a benchmark.
