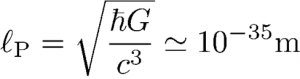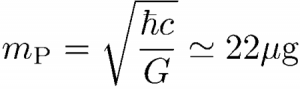QUANTUM/RELATIVITY BORDER
PEOPLE
Astrid Lambrecht
Serge Reynaud
The problem of vacuum energy has been laid out since 1916 and it has no satisfactory solution today. This suggests to pay attention to situations where vacuum fluctuations manifest themselves as measurable effects. An archetype of these effects is the Casimir force which appears between two mirrors as a consequence of their coupling to the radiation pressure of vacuum fluctuations. A dynamical counterpart is the dynamic Casimir effect arising when mirrors are moving in quantum vacuum.
Empty space also contains gravitational field fluctuations, in particular the gravitational waves now observed directly by the LIGO/VIRGO collaboration. These waves induce a universal mechanism of gravitational diffusion which plays a role in the quantum/classical transition, through an efficient decoherence of macroscopic motions. The interplay between quantum physics and relativistic physics is also involved in experimental tests using quantum sensors such as atomic clocks or interferometers.
Experiments such as gravitational wave detection or test of the equivalence principle have motivated a close investigation of quantum limits in ultra-sensitive measurement systems. A related interface between quantum physics and relativity involves the analysis of localization in space-time or clock synchronization procedures, as such procedures are operationally built up on transfers of electromagnetic signals which have to obey the requirements of quantum physics as well as relativity.
Dynamical Casimir effect
Vacuum field fluctuations exert radiation pressure on mirrors in quantum vacuum. When a single mirror is at rest in vacuum, the resulting force vanishes for reasons of symmetry. When it is moving, radiation pressure leads to a dissipative force acting against the motion as soon as the mirror has a non-uniform acceleration. Accordingly the electromagnetic field does not remain in the vacuum state but photons are emitted by the mirror into vacuum. The radiation is called Dynamical Casimir effect (DCE) or Casimir radiation.
The emission of photons can be interpreted using analogies with optical parametric processes. Photon production by the oscillating mirror results from the opto-mechanical coupling between vacuum fluctuations and the mechanical motion. In a linear approximation, the mechanical excitation of frequency Ω is transformed into two photons of frequency ω and ω’ emitted into vacuum. Energy conservation imposes the sum of the photon frequencies to be equal to the oscillation frequency. In vacuum only spontaneous parametric processes can take place as it is impossible to extract energy from vacuum.
Il would be very interesting to show experimental evidence for this Casimir radiation. The orders of magnitude, very small in the case of a single mirror, are largely enhanced when a moving cavity is studied. Photons which are emitted into a cavity mode are resonantly enhanced by the cavity finesse F. The enhancement effect takes place not only when the cavity length is modulated but also when the cavity oscillates as a whole while keeping its mechanical length constant.
- Motion induced radiation from a vibrating cavity A. Lambrecht, M.T. Jaekel, S. Reynaud Phys. Rev. Lett. 77, 615 (1996)
One can demonstrate rigorously the analogy between the dynamical Casimir effect and parametric processes in Quantum Optics by performing a semi-classical analysis of the field propagation inside the non-linear crystals pumped by laser beams. By conveniently choosing the arrangement of these crystals, it is possible to chose devices scattering the field in exactly the same manner than two mirrors oscillating mechanically.
- Analogue Casimir Radiation using an Optical Parametric Oscillator, F.X. Dezael, A. Lambrecht, Europhysics Letters (EPL) 89 (2010) 14001
For a high finesse cavity, it is necessary to take into account the non-linear effects in the interaction at the same time as the cavity losses. Surprisingly these calculations may be performed analytically by using homographies. They show that the field is concentrated into intense short pulses emitted by the cavity at regularly spaced time intervals. Furthermore a process of frequency up-conversion takes places in the opto-mechanical coupling between vacuum fluctuations and the mechanical motion. Photons can be emitted at frequencies higher than the mechanical excitation frequency, which correspond to the cavity modes. On the other hand, no photons are emitted at multiple integers of the mechanical oscillation frequency. 
- Frequency up-converted radiation from a cavity moving in vacuum, Lambrecht A., Jaekel M.T., Reynaud S., Eur. Phys. J. D 3, 95-104 (1998)
- Electromagnetic pulses from an oscillating high finesse cavity: possible signatures for dynamic Casimir effect experiments, A. Lambrecht, Journ. Opt. B 7, 3 (2005)
Quantum/classical boundary and gravitational waves
For any measurement, there should exist an ultimate sensitivity limit at the level of the Planck length, which is the length scale built up with the constants fundamental associated with gravity (G), relativity (c), and quantum physics (h). In most quantum gravity models, it appears as the scale of quantum fluctuations of gravity. This suggests that ultimate quantum fluctuations of an object with a mass m have different behaviors depending whether the associated Compton wavelength is smaller or larger than Planck length.
It follows from this simple reasoning that masses fall in two categories, depending on their values with respect to Planck mass, the mass scale built up with the same fundamental constants. It is quite remarkable that this mass has a value of 22 µg lying on the border between microscopic and macroscopic masses. This coincidence could indicate that the fluctuations of the gravitational field are related to the classical behavior of macroscopic objects. In order to discuss this qualitative idea, we have developed a complete theoretical model of the diffusion and decoherence processes associated with the scattering of stochastic gravitational waves present in our environment. The numbers appearing in this model can be fully characterized within the standard theories of physics by using only existing knowledge.
For the decoherence of macroscopic motions, say the planetary motion of the Moon around the Earth, this gravitational mechanism has a much larger contribution than other possible mechanisms although the coupling to gravitational waves has a negligible on the relaxation of the mean motion. This paradox comes from the fact that the effective temperature associated to the gravitational environment is extraordinarily large.
- Gravitational decoherence of planetary motions, S. Reynaud, P.A. Maia Neto, A. Lambrecht , M.-T. Jaekel, Europhys. Lett. 54 135 (2001)
In spite of this very large effective temperature, the gravitational decoherence mechanism has a negligible influence on microscopic motions such as those of the fields involved in atomic interferometers, essentially because microscopic masses are indeed very small compared with Planck mass. This conclusion holds even for the matter-waves interferometers working with large-mass molecules.
- Ultimate decoherence border for matter-wave interferometry, B. Lamine, R. Hervé, A. Lambrecht, S. Reynaud, Phys. Rev. Lett. 96 050405 (2006)
The same question is at the heart of the proposed space mission Macroscopic Quantum Resonators (MAQRO). The project harnesses recent developments in quantum opto-mechanics, high-mass matter-wave interferometry as well as state-of-the-art space technology to push macroscopic quantum experiments towards higher mass matter-wave interferometry.
- Macroscopic quantum resonators (MAQRO): update 2015, R Kaltenbaek, M Aspelmeyer, PF Barker, A Bassi, J Bateman, Kai Bongs, S Bose, C Braxmaier, Č Brukner, B Christophe, M Chwalla, P-F Cohadon, AM Cruise, C Curceanu, K Dholakia, L Diósi, K Döringshoff, W Ertmer, J Gieseler, N Gürlebeck, G Hechenblaikner, A Heidmann, S Herrmann, S Hossenfelder, U Johann, N Kiesel, M Kim, C Lämmerzahl, A Lambrecht, M Mazilu, GJ Milburn, H Müller, L Novotny, M Paternostro, A Peters, I Pikovski, AP Zanoni, EM Rasel, S Reynaud, CJ Riedel, M Rodrigues, L Rondin, At Roura, W P Schleich, J Schmiedmayer, T Schuldt, KC Schwab, M Tajmar, GM Tino, H Ulbricht, R Ursin, V Vedral, EPJ Quantum Technology 3 (2016) 5
We have also studied how quantum correlations survive at large scales in spite of their exposition to stochastic backgrounds of gravitational waves. Considering Einstein-Podolski-Rosen (EPR) correlations built up on the polarizations of photon pairs and evaluating how they were affected by the gravitational wave backgrounds, we did show that their decoherence remains small and that EPR correlations can in principle survive up to the largest cosmic scales.
- Large-scale EPR correlation and gravitational waves backgrounds, B. Lamine, R. Hervé, M.-T. Jaekel, A. Lambrecht, S. Reynaud, EPL 95 20004 (2011)
Lecture notes containing a general review on these topics can be found there with numerous references :
- Gravitational waves, diffusion and decoherence, S. Reynaud, B. Lamine, M.-T. Jaekel, International School of Physics Enrico Fermi on Atom Optics and Space Physics (Varenna, 2007) in Atom Optics and Space Physics, p. 219-239 (Societa Italiana di Fisica & IOS Press, 2009) or in arXiv
Atomic clocks as quantum space-time sensors : ACES
A good understanding of the interface between quantum physics and gravity is particularly important for atomic clocks used to measure Einstein redshift. This effect, a key prediction of general relativity, states that gravity affects the clock in a universal manner. It plays an important role in metrology and it has been tested with good accuracy in several experiments. An improved accuracy for this test is the main objective of the ACES project, which aims to embark a cold atomic clock on the International Space Station.
- Testing General Relativity with Atomic Clocks, S Reynaud, C Salomon, P Wolf, Space Science Review 148 233 (2009)
In 2010, the team of Steven Chu suggested that atomic interferometry experiments measured the redshift on the quantum clock operating at the Compton frequency that is associated with the rest mass of the atom of cesium. This interpretation would have implied that the redshift test was done with a precision greater than the goal of ACES. However it drew fundamental criticism and sparked a controversy that continues today.
This led us to develop a theoretical collaboration with P. Wolf and C.J. Bordé (SYRTE), L. Blanchet (IAP), C. Salomon and C. Cohen-Tannoudji (LKB) to analyze in detail the significance of gravity tests that are performed on measurements of phase shift of quantum fields. The main result of this analysis was that the atomic interferometry experiments discussed by Steven Chu et al essentially measure the acceleration of atoms in free fall with respect to the experimental platform. They are interesting as tests of the universality of free fall for atoms, but not as clock tests.
- Atom gravimeters and gravitational redshift, P. Wolf, L. Blanchet, C.J. Bordé, S. Reynaud, C. Salomon, C. Cohen-Tannoudji, Nature 467 E1 (2010)
- Does an atom interferometer test the gravitational redshift at the Compton frequency ?, P. Wolf, L. Blanchet, C.J. Bordé, S. Reynaud, C. Salomon, C. Cohen-Tannoudji, Class. Quant. Grav. 28 145017 (2011)
- Reply to the comment on Does an atom interferometer test the gravitational redshift at the Compton frequency ?, P. Wolf, L. Blanchet, C.J. Bordé, S. Reynaud, C. Salomon, C. Cohen-Tannoudji, Class. Quant. Grav. 29 048002 (2012)
Two news accompanied this work on the web
Atomic interferometers and relativity : MIGA
Our group is involved in the Matter wave – laser based Interferometer Gravitation Antenna (MIGA) project of a novel infrastructure to study space-time curvature and gravitational waves. Using atomic interferometry techniques, this infrastructure will lead to new applications extending from monitoring the evolution of the Earth gravitational field to providing a new tool for detecting gravitational waves. It constitutes a fully new tool combining the methods of quantum mechanics and relativity for ultra-sensitive measurements in geophysics as well as fundamental physics.
- Exploring gravity with the MIGA large scale atom interferometer, B. Canuel, A. Bertoldi, L. Amand, E. Borgo di Pozzo, B. Fang, R. Geiger, J. Gillot, S. Henry, J. Hinderer, D. Holleville, G. Lefèvre, M. Merzougui, N. Mielec, T. Monfret, S. Pelisson, M. Prevedelli, S. Reynaud, I. Riou, Y. Rogister, S. Rosat, E. Cormier, A. Landragin, W. Chaibi, S. Gaffet, P. Bouyer Scientific Reports 8:14064 (2018)
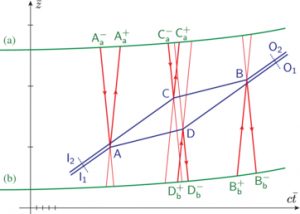
Space-time diagram for an atomic interferometer in the free fall frame. Blue, red and green lines represent the motions of atoms, light and laser sources, respectively.
Our group has discussed the quantum phase observable measured by a large scale atomic interferometer in a fully relativistic context. We have written it in terms of laser phases which are invariant under relativistic gauge transformations. The phase shift is the sum of light and atomic contributions which are connected to one another through their interplay with conservation laws at the interaction vertices.
In the case of a closed geometry, we have written a new compact form of the phase shift in terms of a Legendre transform of the laser phases. We have illustrated these general expressions by discussing the techniques commonly used for compensating the Doppler shift.
- Phases and relativity in atomic gravimetry, M.-T. Jaekel, B. Lamine, S. Reynaud Class. Quantum Gravity 30 065006 (2013)
Quantum limits in GW detectors and MICROSCOPE
Quantum noise limits the sensitivity of interferometric length measurements. It is generally admitted that it leads to an ultimate sensitivity, the standard quantum limit (SQL). In a detailed analysis of quantum noise, we have shown that a judicious use of squeezed states allowed one to push the sensitivity beyond this limit. This general method will certainly be applied some day for gravitational wave detection.
- Quantum limits in interferometric measurements, M.-T. Jaekel, S. Reynaud, Europhysics Letters 13 (1990) 301
Beyond the SQL, quantum fluctuations still result in limitations which are determined by irreducible fundamental mechanisms. For macroscopic reflectors, the quantum noise on positions is dominated by gravitational vacuum fluctuations, and it takes a universal form deduced from quantum fluctuations of space-time curvatures in vacuum, which fixes ultimate quantum limits in spacetime measurements.
- Quantum limits in spacetime measurements, M.-T. Jaekel, S. Reynaud, Quantum and semiclassical optics 7 (1995) 639
The space test of the equivalence principle, MICROSCOPE, uses active techniques to control noise, cold damping to reduce thermal noise, drag free mode to eliminate the perturbations exerted on the satellite. Using a quantum network theory developed in our group, we have calculated the sensitivity limits of the capacitive accelerometers developed at ONERA for this test. We were able to prove that these active techniques did work even in the quantum regime, allowing one to add damping without reducing the measurement sensitivity.
- Quantum theory of fluctuations in a cold damped accelerometer, F. Grassia, J.-M. Courty, S. Reynaud, P. Touboul, Eur. Phys. J. D 8:101 (2000)
Navigation in space-time and quantum physics
Quantum operators corresponding to the time references exchanged in synchronization procedures can be defined by using the conformal symmetry of Maxwell equations. Since this symmetry includes transformations to accelerated frames, the shifts of these operators under such frame transformations are also obtained. They differ from the classical laws while ensuring compatibility of transformations of time and frequency references.
Quantum operators associated with localization of an event in space-time can be introduced analogously, for example as intersections of light rays. The position of the event is a vector containing four observables associated with localization in time and the three spatial directions. In contrast with common statements, there effectively exists an operator representing a position in time and it is conjugated to energy.
Mass being the Lorentz invariant built on energy-momentum, its variation under transformations to accelerated frames is given by the position observables, in full consistency with the principle of equivalence between acceleration and gravity. The redshift of energy-momentum depends on position observables but also on the spin associated with the quantum state under study. Components of this spin also determine the commutators of space-time position observables. Although they differ from the laws of classical relativity, these quantum laws possess the same universality character. Furthermore, they allow one to describe metrical relations for the observables.
Localization observables may be defined analogously for an electron. In the algebraic generalization of the Dirac theory obtained in this manner, not only positions in space and in time but also mass are quantum operators. The redshift of mass is that of a quantum conformal factor consistent with the Einstein equivalence principle. Like in the case of photon, an electron remains an electron under transformations to accelerated frames.
Localization of electrons in space-time can be described in terms of quantum observables which correspond to the hexaspherical variables of classical projective geometry and are directly compatibles with conformal symmetry. This representation allows one to write the law of free fall under the same quantum form in accelerated as well as inertial frames.
A number of references can be found in the review articles
- Quantum Observables associated with Einstein Localization, M.-T. Jaekel, S. Reynaud, in Frontier Tests of QED and Physics of the Vacuum, E.Zavattini, D.Bakalov and C.Rizzo eds., (Heron Press,1998) 389-404 [in the arXiv]
- Quantum algebraic representation of localization and motion of a Dirac electron, M.-T. Jaekel, S. Reynaud, in QED and Physics of the Vacuum, G. Cantatore ed. (AIP Conference Proceedings, 2001) 58-67 [in the arXiv]
- Conformal symmetry and quantum localization in space-time, M-T Jaekel, S Reynaud, In Geometrical methods in physics, AIP Conference Proceedings 956, P. Kielanowski,A. Odzijewicz, M. Schlichenmaier, T. Voronov eds., (2007) 61-72 [in the arXiv]
- Mass, Inertia, and Gravitation, M-T Jaekel, S Reynaud, in Mass and Motion in General Relativity, L. Blanchet, A. Spallicci and B. Whiting eds. (Springer, 2011) 162 491-530 [in the arXiv]