Scientific context
Our group, the multimode quantum optics group of Laboratoire Kastler Brossel, pioneered many aspects of continuous variable (CV) approach to quantum optics. Our main objects of interest are the quadratures of the electric field, which are typically measured through homodyne detection. Our activities generally span both spatial and spectral modes, which we manipulate to develop tools for quantum computation, communication, and metrology.
Our general objective is the creation of multimode squeezed states of optical pulses, either by a synchronously pumped optical parametric oscillator (SPOPO) [1], or through nonlinear waveguides. As such, our sources can create big entangled Gaussian states, which can be probed in arbitrary modes by shaping the local oscillator of the homodyne detector. In recent years, we have gradually explored mode-selective photon subtraction and addition, which allows us to generate multimode non-Gaussian states of light in a highly versatile way [2].
Apart from our experimental focus, the group also has purely theoretical activities where the framework of CV quantum optics is further developed. In particular for non-Gaussian quantum states, there are still many fundamental questions that remain unanswered [3]. The interplay between theoretical work and experiments is a key element of our group.
Project
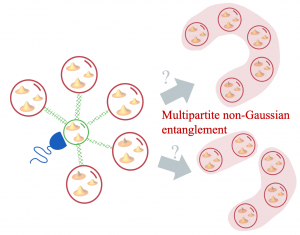
These theoretical activities are at the core the proposed post-doctoral project, which aim to unravel properties of non-Gaussian states. In particular, we focus on the study of non-Gaussian entanglement, i.e., quantum states where the quantum correlations themselves are of a non-Gaussian nature. This entanglement may be understood as a type of quantum correlations that cannot be witness based on the covariance matrix of the state. We previously showed the existence of such non-Gaussian quantum correlations in pure photon-subtracted states [4], but are currently lacking a more general theoretical framework to study its properties.
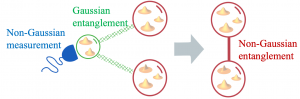
Conceptual scheme to create non-Gaussian entanglement
Your role as a post-doc is to help develop witnesses and measures for non-Gaussian entanglement, tailored towards multipartite systems ideally compatible with the group’s experimental capabilities. You will then apply these techniques to explore applications of non-Gaussian entanglement. Depending on your background, the applications could be aimed at various quantum technologies, ranging from quantum computing to quantum metrology.
Possible starting points for the work include the use of metrology-based entanglement witnesses [5], phase space methods [3], techniques from network theory [6,7], and more brute-force machine-learning techniques [8]. However, we encourage candidates to use their past experience the pursue alternative routes.
Environment
As a whole, the group has a tradition of working together with a diverse range of people from very varied backgrounds. This diversity often leads to fruitful scientific input from different points of view, and it allows the group to explore new avenues. This has, for example, led to a growing activity in theoretical work over the past few years. The strength of our group is the constructive interplay between all these different points of view. Furthermore, the moderate size of our group gives PhD students and postdocs the opportunity to discuss with PIs on a daily basis. This gives rise to a dynamical atmosphere with a lot of space for discussion.
In your day to day activities, you will participate in the supervision of PhD students who work on theoretical topics and interact with the experimentalists in the group. Your work fits in the ANR project “NoRdiC”, which provides support to enlarge your scientific network and establish new international collaborations.
Practical information
- Application process: CV and motivation letter to be uploaded to CNRS portal
- Application deadline: 16/02/2022.
- Starting date: we aim for 01/06/2022 but are flexible
- Duration of contract: Two years
- Salary: Monthly net salary between 2100€ and 2800€, depending on experience
- For more information: walschaers@lkb.upmc.fr
References
[1] J. Roslund, R. M. De Araujo, S. Jiang, and C. Fabre, Nature Photonics 8, 109 (2014).
[2] Y.-S. Ra, A. Dufour, M. Walschaers, C. Jacquard, T. Michel, C. Fabre, and N. Treps, Nature Physics 16, 144–147 (2020).
[3] M. Walschaers, PRX Quantum 2, 030204 (2021).
[4] M. Walschaers, C. Fabre, V. Parigi, and N. Treps, Phys Rev Lett 119, 183601 (2017).
[5] M. Gessner, L. Pezzè, and A. Smerzi, Quantum 1, 17 (2017).
[6] G. García-Pérez, M. A. C. Rossi, B. Sokolov, E.-M. Borrelli, and S. Maniscalco, Phys. Rev. Research 2, 023393 (2020).
[7] M. Walschaers, N. Treps, B. Sundar, L. D. Carr, V. Parigi arXiv:2012.15608
[8] V. Cimini, M. Barbieri, N. Treps, M. Walschaers, and V. Parigi, Phys. Rev. Lett. 125, 160504 (2020).

Recent Comments