Compression des états quantiques multimodes pour améliorer les réseaux de capteurs
La nature probabiliste de la mécanique quantique nous empêche généralement de prédire avec certitude le résultat d’une mesure individuelle. Ces fluctuations quantiques conduisent à un bruit de mesure qui limite la précision de toute mesure, même après que toutes les sources de bruit technique ont été éliminées, par exemple en isolant l’expérience de son environnement.
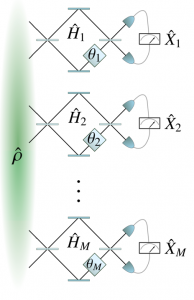
Figure 1. Représentation schématique d’un réseau de capteurs basé sur M interféromètres parallèles. Chaque interféromètre capture un paramètre différent. La sensibilité d’une estimation collective de tous les paramètres peut être améliorée par la compression des observables de mesure locaux et par des corrélations quantiques entre les interféromètres
Pour dépasser la limite de précision imposée par le bruit de mesure, le domaine de la métrologie quantique explore le potentiel offert par les idées de la théorie de l’information quantique. Par exemple, en concevant des états quantiques non classiques, il est possible de réduire les fluctuations quantiques de l’observable mesurée en augmentant celles d’un autre observable qui n’a aucun intérêt pour la mesure. Cette technique, connue sous le nom de « compression », est utilisée aujourd’hui pour améliorer la sensibilité des détecteurs d’ondes gravitationnelles ainsi que des horloges et des interféromètres atomiques. Dans ces expériences, un seul paramètre de phase est mesuré avec la plus grande précision possible.
Ayant établi une assez bonne compréhension de la théorie de la métrologie quantique des paramètres uniques, les chercheurs ont récemment commencé à aborder la question des limites de précision pour les réseaux de capteurs qui mesurent plusieurs paramètres simultanément. Ce problème est d’une grande pertinence pour le développement de méthodes d’imagerie quantique et la mesure de champs électromagnétiques distribués spatialement et de leurs gradients. Cependant, les limitations fondamentales du cadre théorique existant rendent très difficile l’identification des limites de précision dans les scénarios généraux
Dans une récente collaboration entre le LKB et des chercheurs du CNR (Florence, Italie), nous avons développé une méthode théorique qui caractérise la compression de multiples observables quantiques. Le gain de sensibilité qui peut être obtenu dans une mesure multiparamétrique est exprimé en termes d’une matrice de compression qui capture les erreurs de tous les paramètres et les corrélations entre eux. Notre travail établit les outils théoriques nécessaires pour comprendre le potentiel des états comprimés dans les systèmes multimodes pour les mesures multiparamétriques. Il fournit en outre une approche pratique pour le développement de réseaux de capteurs basés sur des systèmes quantiques atomiques et optiques.
Article complet : M. Gessner, A. Smerzi, L. Pezzè, Multiparameter squeezing for optimal quantum enhancements in sensor networks, Nature Communications 11, 3817 (2020)
