COLD ATOMS IN RANDOM POTENTIALS
Anderson localization of matter waves, Coherent back and forward scattering, Wave-packet dynamicsPublications
- [1] D. Delande, G. Orso, Mobility Edge for Cold Atoms in Laser Speckle Potentials, Phys. Rev. Lett. 113, 060601 (2014)
- [2] M. Pasek, Z. Zhao, D. Delande, G. Orso, Phase diagram of the three-dimensional Anderson model for short-range speckle potentials, Phys. Rev. A 92, 053618 (2015)
Mobility edge in speckle potentials
 The team is mainly interested in the behavior of cold atoms in the presence of optical random potentials, in particular in the regime where Anderson localization occurs (see also our recent results on dynamical localization). Recently, this problem has been the subject of intensive experimental activity aiming to precisely measure the position of the mobility edge, which separates the metallic from the insulating regime in the Anderson transition.
The team is mainly interested in the behavior of cold atoms in the presence of optical random potentials, in particular in the regime where Anderson localization occurs (see also our recent results on dynamical localization). Recently, this problem has been the subject of intensive experimental activity aiming to precisely measure the position of the mobility edge, which separates the metallic from the insulating regime in the Anderson transition.
In many experiments, cold atomic gases are exposed to a laser light that has been transmitted or reflected through a diffusive plate. The resulting random potential is a speckle, whose statistics is characterized by an asymmetric (exponential) distribution and a non-vanishing correlation length. These peculiar properties imply a large asymmetry in the position of the mobility edge and in the shape of spectral functions for blue and red speckle potentials. Furthermore, the position of the mobility edge has nothing in common with the one that could be expected for usual Gaussian or uncorrelated random potentials.
Recently, we have numerically computed the precise position of the mobility edge of atoms exposed to a continuous speckle potential and have studied its dependence versus the disorder strength and correlation function, thus providing a guide for future experiments [1]. This question has also been investigated in three-dimensional disordered optical lattices [2].
Publications
- [1] T. Karpiuk et al., Coherent Forward Scattering Peak Induced by Anderson Localization, Phys. Rev. Lett. 109, 190601 (2012)
- [2] S. Ghosh et al., Coherent forward scattering in two-dimensional disordered systems, Phys. Rev. A 90, 063602 (2014)
Coherent forward scattering
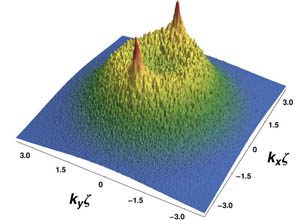 When a wave is scattered phase coherently in a disordered environment, phase information is not lost, only converted into an intricate interference pattern. After averaging over randomness, interference is scrambled except in the backscattering direction of the velocity distribution where there is a narrow peak, a phenomenon known as coherent backscattering (CBS).
When a wave is scattered phase coherently in a disordered environment, phase information is not lost, only converted into an intricate interference pattern. After averaging over randomness, interference is scrambled except in the backscattering direction of the velocity distribution where there is a narrow peak, a phenomenon known as coherent backscattering (CBS).
We have recently shown that when the wave propagates in even stronger disorder and begins to halt its progression due to Anderson localization, the CBS signal is complemented by a spectacular peak in the opposite, forward direction. At long times, the velocity distribution freezes into a symmetric, twin-peak structure, retaining a long-term memory of the initial direction. This coherent forward scattering (CFS) signal has been discovered by numerically studying the velocity distribution of a wave packet launched inside a random potential, as done in present-day cold-atom experiments. At short times, a perturbative theoretical explanation based on the interference effect that is already responsible for CBS has been proposed [1]. At long times, the description of the CFS peak requires to use a non-perturbative approach [2].
Coherent forward scattering is expected to be quite general, observable with many different types of waves under the right circumstances. Further studies will certainly improve our understanding of the behavior of waves when they undergo Anderson localization.
